티스토리 뷰
이전의 글 산업별 총자본경상이익률의 충격반응함수 추정 에서 나는 코스닥의 부문별 총자본경상이익률을 마르크스경제학적 이윤율의 대체지표로서 활용하여 각 부문의 이윤율 변수들이 상호영향을 받고 있다는 점을 확인한 바 있다.
이번 글에서 나는 이윤율의 균등화를 간접적으로 확인하고자 공적분 분석과 벡터오차수정모형(VECM)을 활용하여 이것이 균형안정적인지를 확인하고자 한다. 여기서 균형안정적이라는 말은 최적균형을 의미하지 않는다. 단지 중심에서 이탈한다 하더라도 다시 복귀하는 "안정성"을 말하는 것이다.
그런데 마르크스경제학의 이윤율은 이론적으로 최적화를 요구하는 것은 아니며 이윤율이 자본간 경쟁에 따라 균등화 혹은 균등화를 향해 나아간다는 성질만 밝혀내는 것으로도 충분하다. 따라서 이는 곧 이윤율 변수들이 균등화를 향해 나아간다는 전제와 중심이 같은 의미로 둘 때 이윤율의 어떤 충격 등에 의해 중심에서 이탈할 때 다시 이를 중심으로 복원하는 '속도조정계수벡터'의 유의성만 판가름하면 될 것이다.
1. 데이터의 취득 및 I(1)
데이터는 산업별 총자본경상이익률의 충격반응함수 추정에서 얻었던 데이터 그대로 사용한다. 단 여기서는 1차 차분한 데이터가 아니라 원형 그대로 사용한다. 왜냐하면 함부로 차분할 경우 그것이 가지고 있던 공적분 관계까지 희생될 수 있기 때문이다. 또한 VECM은 VAR모형과 달리 시계열적 안정성을 요구하지 않는다. 다만 공적분 관계가 $n$ 개의 변수에 대해 하나 이상에서 $n-1$ 개가 존재해야 한다. 그 외에는 공적분 분석은 의미가 없다.
예컨대 $x_{t}$와 $y_{t}$라는 시계열 변수가 있는데 이것이 $x_{t},y_{t}~I(1)$, 즉 1차 차분에서야 시계열적 안정성(평균과 분산이 시간에 대해 일정한)을 획득할 수 있는 시계열적으로 불안정한 변수라고 하자. 그런데 이들을 다음과 같이 공적분 방정식으로 정의하면 시계열적 안정성을 갖는 변수 $e_{t}$를 갖게 되는 경우가 존재할 수 있다.1
$e_{t}=\beta_{1}x_{t}+\beta_{2}y_{t}$
단위근이 존재하는 데이터는 계량경제학자들을 지속적으로 괴롭혀왔고 1차 차분을 하는 경우 데이터가 갖는 장기적인 변화들을 희생하게 되는 단점이 있었다. 이러한 문제를 해소하는 문제로써 공적분 방정식이 유용하게 활용되어왔던 것이다.
그런데 우리가 사용하는 데이터의 변수는 총 29개의 산업으로 이루어져있다. 너무 많은 변수는 모형의 복잡도를 증가시켜 비효율을 낳으며 이것이 컴퓨터 계산을 통해 해소된다하더라도 다중 회귀분석에서는 변수 수가 추가되면 추가될수록 결정계수인 $R^{2}$이 증가하는 경향이 강하다. 왜냐하면 잔차제곱합 SSE가 작아지기 때문이다.2 본 연구는 종속변수를 설명하기 위한 모형이 목적이 아니므로 모든 변수들의 특성을 되도록이면 살리면서 변수의 수를 줄일 수 있는 방법의 하나인 인자분석(factor analysis)을 활용할 것이다.
2. 인자분석
인자분석(FA)은 독립변수들에서 잠재적인 변수를 추려내는 방법이다. 인자분석과 주성분분석은 비슷한 점이 많긴 하지만 같지는 않다. 주성분분석은 공분산행렬의 고유값과 고유벡터를 이용하여 통계분석자의 주관과 상관없이 전체 분산을 설명해주는 주성분 로딩들을 적절하게 선택하는 것이다. 그러나 이에 반해 인자분석은 통계분석자의 주관이 어느 정도 개입되게 된다. 여기서는 독립변수를 잘 설명하는 잠재적인 변수들을 추려내는 것이 목표가 된다. Shin Takahashi(2017)3을 참고할 것.
인자분석은 설명변수들을 잘 설명해주는 잠재적인 변수들을 찾아내는 것이다. 인자분석에서는 주성분분석과 같이 Kaiser 등의 기준에 따라 변수의 수를 선택하는 것이 아니며 그 변수의 수는 임의로 설정된다. 일단 Kaiser 기준에서는 6개, Jolliffe 기준에서는 9개가 나오는데 6개의 인자변수에서는 공적분 관계가 성립하지 못했다는 점에서 이를 기각하고 7개를 선택하였다. 9개의 변수의 경우 그 잠재적 변수를 확인하기가 너무 어려웠기 때문이다.
인자변수의 수를 먼저 선택한 후 아래와 같이 R프로그래밍에 의해 인자변수 로딩을 얻게 되었다. 회전방법은 가장 많이 사용되는 "varimax"를 이용하였다.
> x <- data.matrix(read.csv("04_17월별 코스닥_산업별_수익현황_총자본경상이익률.csv")) > FA <- principal(x, nfactors=7, rotate="varimax"))#인자분석이를 한 눈에 정리하기 쉽도록 네트워크 그래프를 그려보도록 하자. 여기서는 qgraph 패키지를 이용한다. (설치시간이 좀 걸린다. 다만 이는 상관도에 대한 직관적인 그래프도 제공해주며 네트워크 분석 등에 매우 유용한 패키지이다)
> install.packages("qgraph")#설치시간이 오래걸림(7~10분정도?)
> library(qgraph)
> qgraph(FA, layout = "circle")
해당 qgraph의 결과에서 강한 관계로 나타나는 관계들을 표로 정리하였다. 또한 이를 통해 다음과 같이 잠재적 변수들에 명칭을 부여하였다.
| 순번 | 산업명 | 재료및장비 | 재료및정보서비스 | 제약및정보서비스 | IT서비스 | 출판및건설 | 문화서비스및재료 | 건설및운송 |
| RC1 | RC2 | RC3 | RC4 | RC5 | RC6 | RC7 | ||
| 1 | 음식료·담배 | O | ||||||
| 2 | 섬유·의류 | O | ||||||
| 3 | 종이·목재 | O | ||||||
| 4 | 출판·매체복제 | O | O | |||||
| 5 | 화학 | O | O | |||||
| 6 | 제약 | O | ||||||
| 7 | 비금속 | O | ||||||
| 8 | 금속 | O | ||||||
| 9 | 기계·장비 | O | ||||||
| 10 | 일반전기전자 | O | ||||||
| 11 | 의료·정밀기기 | O | ||||||
| 12 | 운송장비·부품 | O | ||||||
| 13 | 기타 제조 | O | ||||||
| 14 | 건설 | O | O | O | ||||
| 15 | 유통 | O | ||||||
| 16 | 운송 | O | ||||||
| 17 | 금융 | O | ||||||
| 18 | 오락·문화 | O | O | |||||
| 19 | 기타서비스 | O | O | |||||
| 20 | 통신서비스 | O | ||||||
| 21 | 방송서비스 | O | O | O | ||||
| 22 | 인터넷 | O | ||||||
| 23 | 디지털컨텐츠 | O | O | |||||
| 24 | 소프트웨어 | O | ||||||
| 25 | 컴퓨터서비스 | O | ||||||
| 26 | 통신장비 | O | ||||||
| 27 | 정보기기 | O | O | |||||
| 28 | 반도체 | O | O | |||||
| 29 | IT부품 | O |
[표 1] 인자변수 로딩과 설명변수인 산업 간의 매칭표
인자변수들을 모두 선별하였으므로 이제는 이를 가지고 공적분 관계가 존재하는 지 확인해보도록 하자.
3. 공적분분석
공적분이란 적분된 변수들의 선형결합에 의해 한 개의 정상시계열인 I(0) 변수가 만들어지는 경우를 말한다.4
즉 위에서 하던 말을 반복하자면 $x_{t}$와 $y_{t}$라는 시계열 변수가 있을 때 다음과 같은 선형결합으로 I(0)인 변수를 만들 수 있을 때 이를 공적분관계라 하며 아래의 식을 공적분 방정식이라고 표현한다.
$e_{t}=\beta_{1}x_{t}+\beta_{2}y_{t}$
우리가 I(0), 즉 정상시계열이라고 하였을 때 이를 시계열적 안정성이라고도 말하는 이유는 이 변수가 시간에 대해 평균과 분산이 일정하기 때문이라는 점을 상기하자. 변수들의 선형결합으로 공적분 관계가 성립한다는 것이란 결국 그 경제적 의미는 장기균형관계를 나타내는 것임을 확인할 수 있다. 따라서 공적분분석은 이러한 장기균형관계를 규명하는 것이기도 하다. 허나 다시 말하지만 이는 최적의 의미는 아니고 커다란 의미에서 중심에서 이탈되더라도 중심으로 회복될 수 있다는 점에서의 안정성을 의미한다.5
이 글에서 우리는 자세한 공적분검정에 대한 내용을 소개하지 않을 것이다. 공적분 검정에는 가장 많이 사용되는 요한슨 검정을 이용하며 그 결과는 다음과 같다. (trace 통계량을 이용하였다)
> x <- FA$scores#인자변수로 변수집합을 재설정
> library(urca)
> jotest=ca.jo(x, type="trace", K=2, ecdet="none", spec="longrun")
> summary(jotest)
###################### # Johansen-Procedure # ######################
Test type: trace statistic , with linear trend Eigenvalues (lambda):
[1] 0.41250533 0.12455991 0.10112877 0.06604477 0.05505472 0.04542962 0.02138198
Values of teststatistic and critical values of test:
test 10pct 5pct 1pct
r <= 6 | 3.44 6.50 8.18 11.65
r <= 5 | 10.83 15.66 17.95 23.52
r <= 4 | 19.83 28.71 31.52 37.22
r <= 3 | 30.70 45.23 48.28 55.43
r <= 2 | 47.65 66.49 70.60 78.87
r <= 1 | 68.80 85.18 90.39 104.20
r = 0 | 153.37 118.99 124.25 136.06요한슨 검정을 시행하면 검정값(test)과 각 유의수준 10% 5% 1%에서의 임계치를 각각 보여주게 된다. 해당 검정값이 각 유의수준에 대한 임계치를 상당수 초과하게 된다면 공적분 관계가 없다는 귀무가설을 기각하게 된다. 위를 보면 $r$이라는 것은 공적분관계로 설정할 수 있는 변수의 수를 이야기한다. 총 변수 수에서 하나를 뺀 수까지 모두 검정하게 된다. 이때 1부터 6까지의 경우 검정값이 모두 임계치들을 초과하지 못하고 있음을 볼 수 있는데, 이는 바로 공적분 관계가 없다는 귀무가설을 기각할 수 없다는 것이다. 그러나 공적분 변수가 없다는 귀무가설을 기각하지 못한다(r=0). 따라서 적어도 한 개 정도는 공적분 관계가 성립할 수 있음을 알 수 있다.
4. 벡터오차수정모형
공적분 관계가 존재하는 체계라면 시계열적 안정성을 위해 1차 차분을 하지 않고도 VAR모형과 같은 체계로 분석이 가능하다고 알려져있다. 이를 벡터오차수정모형(Estimation Of Vector Error Correction Model : VECM)이라고 한다.
먼저 변수들을 $x_{t},y_{t}$라고 한다면 VECM은 다음과 같은 체계로 이루어져있다.
(1) $\binom{\Delta{x_{t}}}{\Delta{y_{t}}}=\binom{a_{1}}{a_{2}}(\beta_{1}x_{t-1}+\beta_{2}y_{t-1})+\begin{pmatrix}\phi_{11,1}&\phi_{12,1}\\phi_{21,1}&\phi_{22,1}\end{pmatrix}\binom{\Delta{x_{t-1}}}{\Delta{y_{t-1}}}+\cdots{}+\begin{pmatrix}\phi_{11,p}&\phi_{12,p}\\phi_{21,p}&\phi_{22,p}\end{pmatrix}\binom{\Delta{x_{t-p}}}{\Delta{y_{t-p}}}+\binom{\epsilon_{1,t}}{\epsilon_{2,t}}$
여기서 (1)식의 우변 첫 번째 항을 보면 일명 조정속도계수라는 것과 공적분방정식의 곱으로 나타나고 있음을 알 수 있다. 조정속도계수 $a_{i}$는 바로 장기균형을 회복할 때의 조정속도를 말한다. 이를 $e_{t}=\beta_{1}x_{t-1}+\beta_{2}y_{t-1}$로 축약하면
(1)' $\binom{\Delta{x_{t}}}{\Delta{y_{t}}}=\binom{a_{1}e_{t-1}}{a_{2}e_{t-1}}+\begin{pmatrix}\phi_{11,1}&\phi_{12,1}\\phi_{21,1}&\phi_{22,1}\end{pmatrix}\binom{\Delta{x_{t-1}}}{\Delta{y_{t-1}}}+\cdots{}+\begin{pmatrix}\phi_{11,p}&\phi_{12,p}\\phi_{21,p}&\phi_{22,p}\end{pmatrix}\binom{\Delta{x_{t-p}}}{\Delta{y_{t-p}}}+\binom{\epsilon_{1,t}}{\epsilon_{2,t}}$
이 되고 $e_{t-1}$은 평균적으로 $x_{t}$가 $a_{1}$만큼 변하고, $y_{t}$가 $a_{2}$만큼 변하도록 만든다.6
그런데 조정속도계수가 0이라면, 중심에서 이탈한다하더라도 어떠한 변화도 일으키지 못하게 된다. 따라서 VECM의 관건은 이 조정속도계수가 0인지에 대해 확인해야 한다.
우리는 적정시차를 AIC기준, SC 기준 모두 1이라는 점을 확인하였으며 tsDyn 패키지의 VECM 함수를 적용하여 이 문제를 확인해보았다. 해당 함수에는 최우추정법(ML)과 2단계 최소제곱법(2SLS)을 모두 지원한다. 최우추정법은 대표본의 경우에서 유효하지만.. 적어도 우리는 샘플을 100개 이상이니 적용할 수 있지 않을까? 싶어 일단 적용해보았다. 또한 2SLS의 결과와도 크게 다르지 않았다.
> vecm.jo <- VECM(x, lag=1, estim="ML", LRinclude="none")
> summary(vecm.jo)
#############
###Model VECM
#############
Full sample size: 161 End sample size: 159
Number of variables: 7 Number of estimated slope parameters 63
AIC -2677.633 BIC -2465.879 SSR 137.1252
Cointegrating vector (estimated by ML):
RC1 RC3 RC2 RC4 RC6 RC7 RC5
r1 1 -0.7261948 0.4403314 2.348981 -0.6442163 -2.035498 -1.01646
ECT Intercept RC1 -1 RC3 -1
Equation RC1 -0.0161(0.0069)* 0.0154(0.0204) 0.1133(0.1465) -0.0381(0.0878)
Equation RC3 0.0146(0.0097) -0.0141(0.0286) 0.0968(0.2057) -0.0347(0.1233)
Equation RC2 -0.0083(0.0063) 0.0031(0.0187) -0.0493(0.1348) 0.0308(0.0808)
Equation RC4 -0.0623(0.0093)*** 0.0280(0.0273) 0.1527(0.1966) -0.0682(0.1179)
Equation RC6 -0.0209(0.0109). 0.0031(0.0321) 0.1733(0.2308) -0.1274(0.1384)
Equation RC7 0.0788(0.0110)*** -0.0250(0.0326) -0.5006(0.2345)* 0.1734(0.1406)
Equation RC5 0.0388(0.0128)** -0.0116(0.0377) -0.2947(0.2715) 0.0831(0.1628)
RC2 -1 RC4 -1 RC6 -1 RC7 -1
Equation RC1 -0.0321(0.1474) -0.0127(0.0699) -0.0157(0.0728) -0.0397(0.0556)
Equation RC3 -0.0969(0.2070) 0.0028(0.0981) 0.0033(0.1022) 0.0427(0.0781)
Equation RC2 0.1106(0.1357) 0.0168(0.0643) 0.0049(0.0670) -0.0621(0.0512)
Equation RC4 0.0837(0.1979) -0.1277(0.0938) -0.0071(0.0977) -0.1033(0.0747)
Equation RC6 -0.1280(0.2323) -0.0527(0.1101) 0.0424(0.1146) 0.0435(0.0877)
Equation RC7 0.0273(0.2360) 0.1110(0.1119) 0.0176(0.1165) 0.1136(0.0891)
Equation RC5 0.0953(0.2733) 0.0681(0.1295) 0.0664(0.1348) 0.1100(0.1031)
RC5 -1
Equation RC1 0.0143(0.0474)
Equation RC3 0.0040(0.0666)
Equation RC2 -0.0291(0.0437)
Equation RC4 -0.0746(0.0637)
Equation RC6 0.0130(0.0748)
Equation RC7 -0.0499(0.0760)
Equation RC5 -0.0005(0.0879)여기서 ECT라는 것이 바로 조정속도계수 값이다. RC3(제약 및 정보서비스), RC2(재료 및 정보서비스)들은 유의하지 않으므로 계수값이 0이라는 귀무가설을 기각할 수 없었다. 다만 RC6(문화서비스 및 재료) 부문은 유의수준이 10%에서 유의했다. 나머지는 5% 내에서 모두 유의한 것으로 파악된다.
VECM은 시계열적 안정성 없이도 VAR모형처럼 쓰라고 만든 거다. 그러니 당연히 충격반응함수도 알아볼 수 있다.
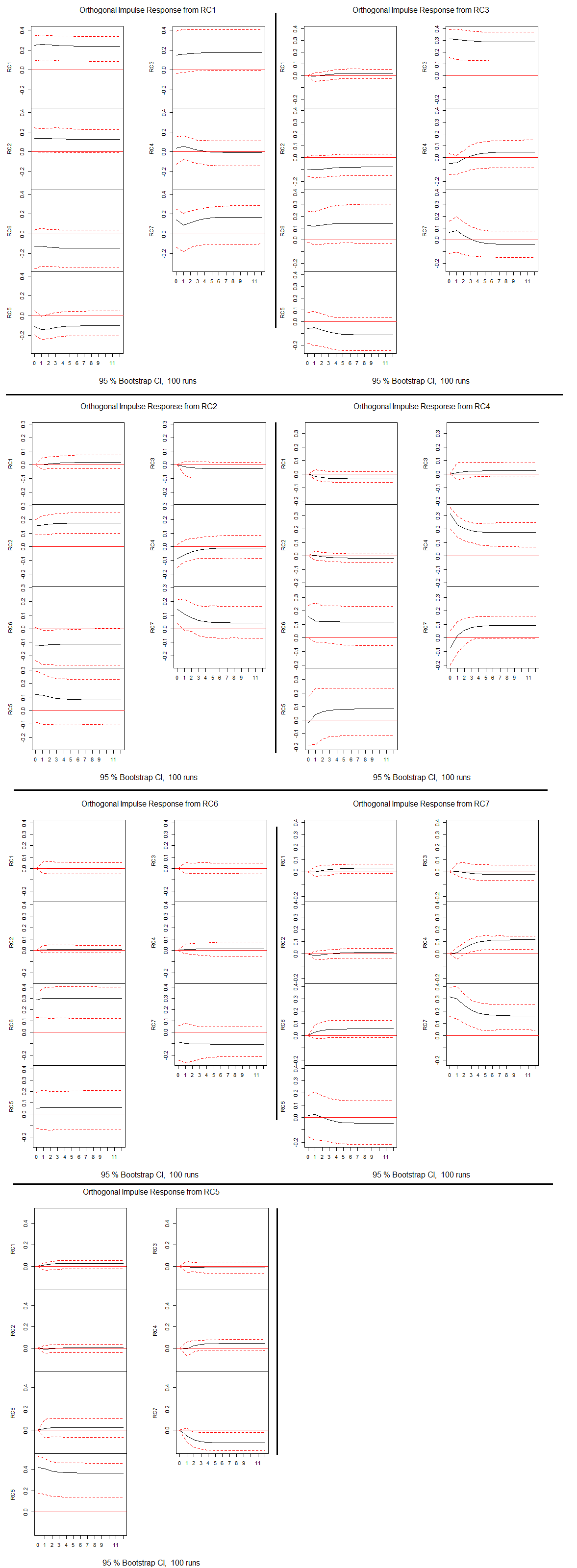
간단히 정리하자면 RC1(재료 및 장비)은 RC4(IT서비스)에 대한 영향이 3개월도 가지 못해 0이 된다. RC3(제약 및 정보서비스)은 RC7(건설 및 운송)에 대해 음의 영향을 미친다. 흥미로운 건 자기 자신에 대해 음의 영향을 내는 부문들이 존재하는데 이는 확률추세가 있는 것은 아닌지 의심스럽게 하는 부분이다. 하지만 이 부분에 대해서는 확인하지 않았다.
5. 결론
해당 체계에서의 균형안정성이 비교적 1차의 시점에서도 매우 유의한 결과가 나온 것을 보면 코스닥에 등록된 산업들은 매우 단기에서도 균형안정성이 높다는 사실을 알 수 있다. 다만 모든 산업이 그런 것은 아닐 것이다. 우리가 만약 이윤율이 모든 부문들 간에 균등화하는 경향을 가정한 후 이러한 균등화 운동에 이탈이 일어난다 하더라도 대체로 산업들은 다시 중심으로 회복하는 경향이 있음을 알 수 있다. 우리는 이로써 VECM을 통해 이윤율 균등화 운동이 존재할만한 근거를 마련함과 동시에 마르크스경제학과 스라파경제학이 중시하는 '생산가격체계'에 대한 실증적 근거를 더 많이 축적해가야 할 것이다. 다만 생산가격체계를 얻었다 하여도 전형문제를 이론적으로 해결하지 않고서는 한 발 나아가긴 어렵다는 점을 감안해야 할 것이다.
[이관 글. 2017-08-04 작성]
'정치경제학' 카테고리의 다른 글
| 소비자선택모형에서 독립변수인 가격이 왜 종축에 있는가에 대한 답 (0) | 2021.05.29 |
|---|---|
| "[자본론]과 경제학체계" 리뷰 (0) | 2021.05.29 |
| 투입-산출모형의 고유값과 고유벡터의 의미 (0) | 2021.05.29 |
| 산업별 총자본경상이익률의 충격반응함수 추정 (0) | 2021.05.28 |
| 직종별 노동자 주성분 분석 - 생산적 노동의 구분을 중심으로 (0) | 2021.05.28 |
