티스토리 뷰
마르크스경제학도 컴퓨터로 시뮬레이션을 하는 연구가 많다. 보통은 이윤율 동학이 많이 다루어진다. 관련된 자료를 뒤져보다보니 브라질의 경제학자 Cláudio Alberto Castelo Branco Puty1학자가 복잡계로 알려진 Cellular Automata(세포 자동자)를 이용하여 이윤율 균등화 가정에 대한 시뮬레이션을 시행한 논문2을 보게 되었다. 사실 개인적으로도 이윤율 균등화 과정을 시뮬레이팅하고싶다는 생각이 있었는데 고맙게도 선행연구가 있던 것이다(아ㅅㅂ 내가 먼저 할 걸). 이걸 보고 무척 독특한 시도라는 생각에 이를 재현해보았다. 그리고 그 의미에 대해 간략하게 해석해보고자 한다.
1. 세포 자동자에 대한 소개
1-1. 세포 자동자란 무엇인가
세포 자동자(이하 CA)에 대해 위키백과 세포 자동자 항목에서 자세한 설명이 나와있다. 더 자세한 것은 [복잡성의 과학]3을 추천한다. 이 방법은 폰 노이만이 자기증식하는 기계를 개념화 하기위해 처음 개발되었다고 한다. CA는 창발적이며 자기조직적인 복잡계의 특성을 갖기 때문에 복잡계의 대표적인 예로 손꼽힌다. 이러한 특성에 따라 인공지능에도 활용되고 있으며 그 응용이 매우 폭넓게 이루어지고 있다고 한다4.
CA는 자신에 대한 특성을 갖고 있다. 그리고 그 자신의 상태를 나타내는 정보를 갖고 있다. 그것은 0과 1로 표현되는 이진 코드일 수 있는데, CA 하나의 상태를 0:Death, 1:Life 같이 나타낼 수 있다는 것이다.
이제 각 CA가 서로에게 영향을 받는 준칙을 마련해보자. 먼저 2차원 평면의 ${n}\times{n}$의 격자. 즉 바둑판을 상상해보자. 여기 판에 올려둔 바둑돌이 바로 CA이다. 여기서 CA가 관측할 수 있는 주변 CA를 무어 이웃이라고 하자. 각각의 세포 자동자는 자신의 주변 가두리 1 길이의 괸측범위를 갖는다고 하자. 그러면 CA는 (주변에 모두 CA 이웃이 있다면) 총 8개의 이웃을 볼 수 있는 것이다. 이때의 이웃을 무어 이웃(Moore Neighborhood)이라고 하며 십자형의 경우 주변 이웃을 폰 노이만 이웃(Von Neumann Neighborhood)이라 한다.
이제 우리는 서로 간에 영향을 받는 관계에 대해 정의할 수 있다. 아래는 그 예시에 불과하다.
- CA의 주위에 아무것도 없으면 외로워서 죽는다.
- CA의 주위에 4개 이상의 CA가 있으면 숨이 막혀 죽는다.
- 그 외의 상황의 경우 세포는 살아남는다.
이런 준칙에 의거하여 임의의 배열 초기값을 설정하고 반복시행을 거치면 자기증식하는 과정을 관찰할 수 있게 된다. 이것이 대표적인 CA 방법이다.
아래는 CA를 공부하고자 파이썬으로 실행해본 결과이다.


간략히 위의 그림을 설명하자면, 2차원 평면이 아니라 1차원 배열을 가지고 루프를 돌려 밑에다 계속 쌓아가는 식으로 생각하면 된다. 세포 자동자의 상호작용에 의해 자기증식화하는 것을 알 수 있다.
1-2. 경제학과 세포 자동자
이제 이를 경제학적인 직관을 이용해 CA를 수정해보자. 이윤율 균등화 작용에 대한 매커니즘을 규명하는 것에 우리는 CA를 이용할 것이다. $N$개의 자본가만 존재하며 2차원 평면 위에 ${n}\times{n}$의 격자 판으로 된 가상의 경제를 가정해보자. 자본가를 무작위로 격자의 셀에 있을 위치를 정한 후 각 자본이 얻고 있는 이윤율이 모두 다른 상태를 갖는다고 하자.
그렇다면 이런 간단한 두 가지 논리로 우리는 자본가가 CA이며, 이윤율은 각 자본가의 상태 정보라는 것을 알았을 것이다.
자본가의 관측 범위에 존재하는 무어 이웃의 상태 값인 이윤율의 차이에 따라 자본가는 자본 이동을 할지 현재 위치를 유지할지를 결정한다. 만약 자본 이동에 아무 장벽이 없다면 이윤율은 균등화될 것이다. 아담 스미스는 이런 간단한 자본가의 행동 준칙만으로 이윤율이 균등화된다고 믿었다. 이는 마르크스도, 신고전파에서도 참으로 받아들여진다. (리카도는 이를 부정했다)
하지만 과연 이 직관은 참인가? 우리는 지금 적절한 방법과 도구를 갖고 있다. 이제 이 도구를 디루기 위한 모형을 마련하고 반복 시행을 시뮬레이팅하여 이 주장을 검증해보도록 하자.
2. Model
2-1. 자본
${n}\times{n}$의 격자-경제를 가정하자. 여기서 자본의 총 가치는 격자의 노드 $(i,j)$에 위치한 개별 자본 $k^{1},\:...\:,k^{n}$(1,...,n은 상첨자이다)의 합으로 정의된다.
(1) $K_{(i,j)}=\sum_{l=1}^{n}k_{(i,j)}^{l}\:\:\:l=1,\:...\:,n$5
여기서 개별자본 각각은 모두 동질하다고 가정된다.
2-2. 이윤율
노드 $(i,j)$ 각각에 이윤율 $r_{(i,j)}$는 비-선형함수로써 자연지수의 멱이 자본의 총가치(부호는 음(-)이다)라는 정의에 따른다.
(2) $r_{(i,j)}=exp(-K_{(i,j)})$6
위에서 설명한 바와 같이 이윤율은 CA의 상태값이 되며 위의 예와 다르게 이진 코드가 아니라 ${0}\leq{r_{(i,j)}}\leq{1}$와 같이 연속적인 범위를 갖는다.
(2)의 정의를 더 잘 이해할 수 있도록 Octave 툴을 이용하여 다음의 그래프를 그려보자. Octave는 Matlab과 호환되는 무료 오픈소스 툴이다.(아! 고마운 존재입니다!)
k = [0:0.1:10]
plot(k,exp(-k),"*")이 코드는 R이나 파이썬에서도 그대로 돌아갈 것이다(아마도?). 코드는 너무 간단해서 설명하지 않겠다. 그러면 다음과 같은 곡선을 볼 수 있다.
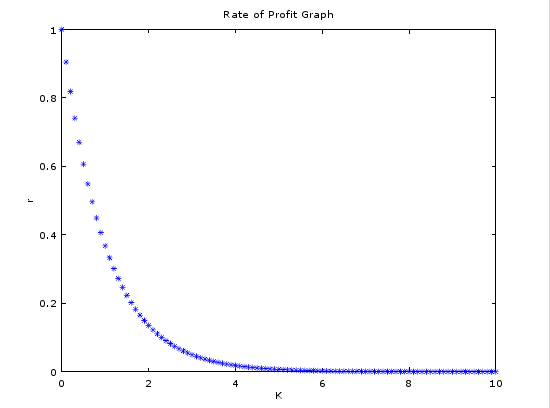
이 곡선의 직관적인 설명은 단순하다. 즉 격자-경제에서 한 셀에 위치한 자본 수가 많을수록 이윤율은 낮아진다는 단순한 사실을 나타냈을 뿐이다.
이로써 우리는 위에서 든 CA의 상태 정보를 이진코드로 나타낸 0:Death와 1:Life를 연속선상에서 생각하면 이윤율이 0에 근접할 수록 자본은 스트레스를 받아서 이동하려 하며 1에 접근할수록 위치를 유지하려고 할 것이란 것을 알 수 있다.
이제 문제는 이동을 할지 말지의 결정할 범주를 정해줘야 한다는 것이다.
2-3. 무어 이웃
우리의 CA의 이웃 범위는 무어 이웃을 사용한다. 이는 이웃이 총 8개의 영역으로 이루어진다.

그런데 이괘모죠.. 우선은 CA의 이웃을 경제학적으로 해석해야 할 것이다. 나는 이것이 자본가의 "촉"이라고 할 것이다. 자본가는 팔랑팔랑 귀이다. 대학동문회 모임이나 중소기업 사장님 협회 회식 때 김모씨가 하는 신사업이 그렇게 잘 되서 이윤율이 존나 높다고 한다. 그래서 비교해보니 자기보다 이윤율이 높고 그런거다. 그래서 막 거기다 투자해버리는.. 그런 귀 얇은 사장을 우리는 가정한다.

그러나 이 격자-경제에서 이동을 할 확률이 존재하고 언제나 반복시행 때마다 이동을 할거라 보기도 어렵다. 그렇기 때문에 정보가 완전하지 않으며 제한적이라고 생각될 수밖에. 논문에서 puty는 이러한 제한이 있음을 인정하지만 CA와 CA의 상호작용 때문에 반복시행 기간이 길어지면 길어질수록 완전정보에 가까워진다고 주장한다7. 이러한 주장은 분명 납득 가능하지만 만약 격자-경제의 규모가 커지게 될 때, 이 가정을 유지할 수 있으려면 비례하게가 아니라 기하급수적으로 더 엄청난 기간이 필요하게 된다. 물론 그렇게 큰 규모의 격자-경제가 필요한지에 대해서 나에게 준비된 답은 없지만 말이다.
어쨌든 무어 이웃은 다음과 같은 조건 하에서 "촉"의 범위가 존재한다.
(3) $N^{Moore}_{i_{o},j_{o}}=[(i,j):|i-i_{o}|\leq{rad},|j-j_{o}|\leq{rad}\:\:\:\:rad=1$
이 논문 저자 puty가 좀 불친절하다. 허나 나는 친절하다(?). (3) 조건문은 프로그래밍을 할 때 유용해보이지만 가두리 하나하나의 위치에 대해 알려주지는 않으므로 좋은 표현은 아니다. 그래서 좀 더 직관성을 높일만한 그림을 그려 보았다.

이러면 코드를 어떻게 짜야할지 감이 오게 된다. 그런데 제일 가에 위치한 경우는? 이를 CA에서는 경계조건이라고 하는데, puty의 경우는 0 경계 조건을 사용하는 것 같다. 즉 가에 있으면 넘어가는 영역은 무시하는 것이다. 익숙하지 않은 언어로 하기는 껄쩍지근하므로 가장 자신있는 C# 코드로 CA의 탐색 알고리즘을 짜보았다.(컴파일은 안 해봤다 참고만 하세요)
public class CellularAutomata
{
public void Main()
{
int n = 10;
for(int i = 0; i < n; i++)
{
for(int j = 0;j<n;j++)
{
for(int s = 0;s<8;s++)
{
// 배열로 가두리 위치 값 정의
int[][] neigh = new int[8][2]{
{-1, -1},{0, -1}, {1, -1}, {1, 0}, {1. 1}, {0, 1}, {-1, 1}, {-1, 0}
};
int i2 = i + neigh[s][0];
int j2 = j + neigh[s][1];
// 가에 위치한 경우 배열 벗어나지 않도록 조건문 구성.
if (i2 >= 1 && j2>= 1 && i2 <= N && j2 <= N)
{
/*여기가 로도스 섬이다! 뛰어라!*/
}
}
}
}
}
}자. "로도스 섬"에서 님들이 해야 할 일은 다음과 같다.
- 사장님 A씨가 고민 중 "음.. 나보다 이윤율이 높은 위치가 있나?"
- 분기 1 : 아 없네. 그냥 존나 가만히 있어야겠다. (A씨 끝. 다음 B 사장님~)
- 분기 2 : 어라? 나보다 겁나 높은 곳이 있어! 어떻하지?("ㅎ" 받침 일부러 했음)
- A 사장님. 여러 변수들 때문에 고민 중.... 할까 말까 할까 말까 할까 말까......
- 어떤 p의 확률로 최대이윤율로 이동. 1-p의 확률로 현 위치 유지(A씨 끝. 다음 B사장님~)
자. 그러면 이제부터 확률함수를 정의하기로 하자.
2-4. Probit 함수
확률함수의 과정은 다음과 같다. 자신의 현 위치의 가두리에서 최대 이윤율이 자신보다 높은 상황이 존재하면 사장님은 그곳으로 자본을 이동한다. 아래의 (4)식은 이를 표현한 것이다.
(4) $[r_{(i_{o},j_{o})}<S_{(i_{n},j_{n})}^{max}\Rightarrow{\forall{k_{(i_{o},j_{o})}^{l}}}\rightarrow{k_{(i_{n},j_{n})}^{l}}\:\:\:\:\:l=1,\:...\:,n$
자본가가 최대이윤율을 가진 집합 $S^{max}$로 이동할 확률은 $p$의 확률로, 이 확률이 다음의 Probit 함숫값과 동일하거나 보다 클 경우에 실제 이동하게 된다.
(5) $\chi=[1+(\frac{1}{1+e^{\alpha{R}-\kappa{k}}})-\epsilon]$
간단하게 자연지수의 멱에 대해서만 살펴보자. 자연지수의 멱인 $\alpha{R}-\kappa{k}$에서 $\alpha$와 $\kappa$는 파라미터이다. $k$는 CA에 있는 자본의 수이며 $R(0\leq{R}\leq{8})$은 CA의 가두리에 존재하는 최대이윤율 $S^{max}$의 수이다. $-\kappa{k}$의 의미는 이런 것이다. 최대이윤율 셀을 인식하는 데는 모두 동일한 기회를 갖고 있다. 그러나 모두가 넘어가게 된다면 <그림3>을 보면 알다시피 이윤율은 하락할 것이다. 따라서 이는 일종의 눈치보는 상황을 반영한다고 보면 되며 자본 이동에 제약이 된다. $\alpha{R}$은 최대이윤율 집합을 관측하는 일종의 기회가 생겼음을 반영한다. 따라서 자본 이동에 유인이 된다. $\epsilon$은 임의적인 충격량으로 무작위로 선택한다. 자세한 건 puty의 논문8을 참고할 것.
3. 결과
자. 이제 준비가 끝났으니 키보드에 손을 올리고 코드를 짜주면 된다. 먼저 개념들을 이해하느라 고생했는데 미안하지만.. 우리가 애초부터 무엇을 하려 했는가. CA로 설정된 자본가가 자본 이동을 확률적으로 행할 것인데, 이때 자기보다 높은 최대이윤율 위치로 이동하게 된다. 이러한 반복시행을 길게 시행할 경우 이윤율 균등화는 일어날 것인가? 그것이 우리가 얻고자 하는 답인 것이다.
이 모형의 특성은 다음과 같다.
- 이윤율은 자본량에 의존한다.
- 자본 이동의 경우 CA의 무어 이웃인 경쟁하는 자본가의 수와 최대이윤율 집합이 존재하는 셀의 수, 그리고 충격량에 의해 확률적으로 결정된다.
- 모든 자본은 동질적이다. (k는 상수로 가정된다)
이제 프로그램을 만들고 적절한 초기조건을 정해야 한다. puty는 여러 파라메터를 통해 결과수치를 비교하지만 나는 아주 단순한 모형을 재현하는데 만족하려 하기 때문에 하나의 예시만을 시행하도록 하겠다.
먼저 파라메터의 경우는 $\alpha=-0.85,\:\kappa=-1$로 정하였다. puty는 이러한 파라메터에 따른 결과를 "Schwartz-Sraffa 궤도"라고 명명하고 있다. 자본가의 총량을 $K$, 그리고 기업-노드의 수를 $N$이라고 하자. puty는 $K=N$인 경우뿐만 아니라 $K\neq{N}$의 경우를 모두 비교하고 있으나(푸념을 하자면.. 내가 영어가 많이 딸리는데.. 브라질 사람이 쓴 영어라서 그런지 읽기가 힘들었다.. 비교를 하는건 좋지만 결과 좀 요약했으면...;;) 나는 $K=N={5}\times{5}=25$로 정하였다. puty는 ${50}\times{50}$으로 하지만.. 싫다. 나는 단순하게 ${5}\times{5}$로 할거야!
이제 프로그램을 짜고 시행해보도록 하자. 일단 확률모형이기도 해서 반복시행 횟수를 기이일게~ 해야 puty의 결과와 비슷할 수 있을거라 생각했기 때문에.. 커피 한잔 먹으며 결과를 기다렸다. (반복횟수는 1,000회정도. puty는 2500회까지 한다. 별로 차이 안나잖아? 그러니 나도 나름 할만큼 한거 같다!) 아무튼 격자-경제에서 자본 이동의 과정을 움직이는 GIF로 만들어서 30회까지의 경과를 나타내보았다.
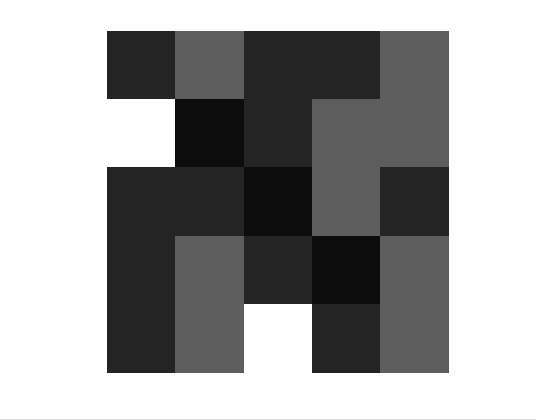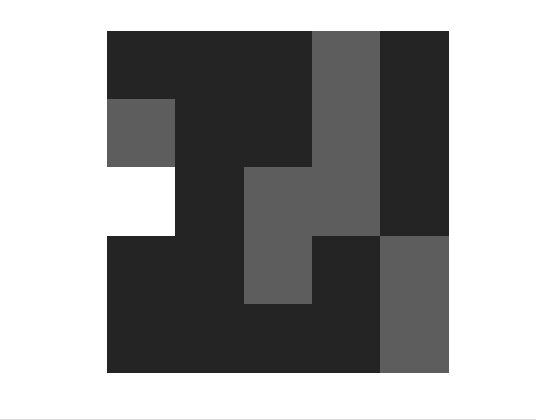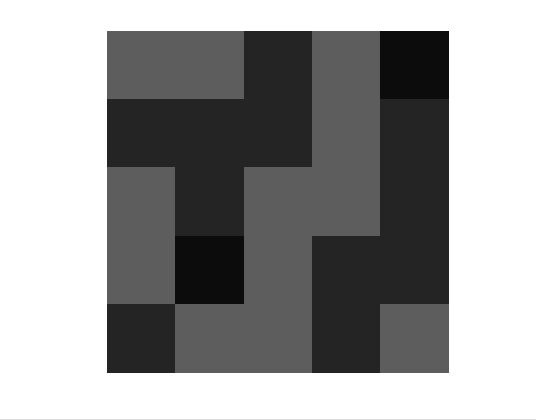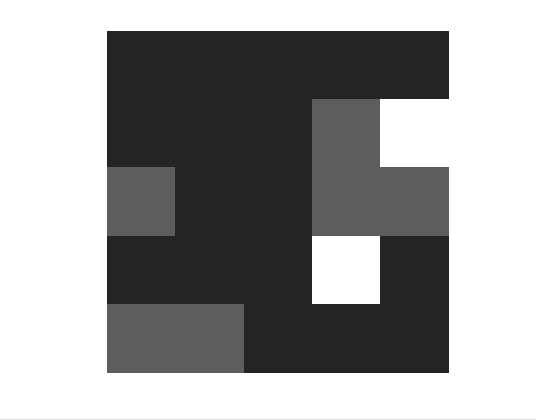
보면 알겠지만 균등화가 전혀 일어나지 않고 무한정 불규칙한 패턴만을 보이고 있다.
그렇다면 이윤율의 기술적 통계를 확인해보는 것도 나쁘지 않을 것이다. 그래서 기술적 통계 추세를 쌓아두도록 프로그래밍 해놓았다. 우선 나는 Skewness, Mean, Variance로 세 가지만 그래프로 나타내었다.
각각에 대해 설명하자면 Skewness는 중심적률이라고 하며 확률분포의 비대칭도를 수치로 나타낸 것이며 음수일 수도 있다. Mean은 말 그대로 전체 이윤율의 평균이며, Variance는 분산으로 기대값(평균,최빈값,중위값)에서 확률변수가 얼마나 떨어져있는지 면적을 수치로 나타낸 것이라고 보면 된다.
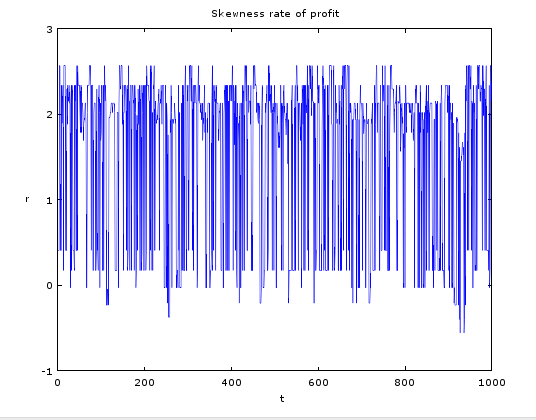
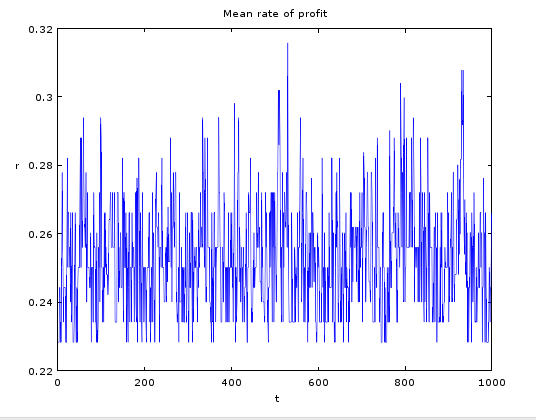
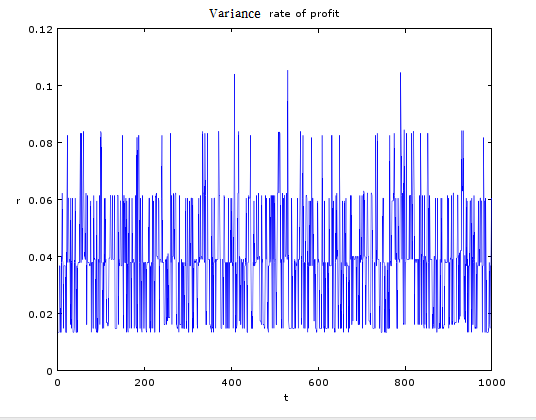
기술적 통계의 내용 역시 안착되는 추세는 나타나지 않고 무한정 와리가리하는 패턴을 보이고 있다. puty는 이러한 결과를 다음과 같이 해석한다.
the result of capital interaction in our artificial economy is the establishment of a never ending oscillation process that becomes a gravitation around a mean of the series a the total number of capitals are increased in the lattice.
우리의 인위적인 경제에서 자본 간 상호 작용의 결과는 (...) 일련의 평균 주변의 인력이 끌어당겨 끝없이 진동하는 과정의 확립이다.9
puty의 말대로 세포 자동자를 이용한 실험결과는 이윤율의 균등화 과정에 대해 부정적인 결론을 이끌어내게 된다. 다만 이윤율 분포의 비대칭성의 경우 음수 주변에서 안착화된다고 한다(내 결과에서는 잘 안 나타나는데.. 내거는 좀 단순하게 한거니까 그렇다치고, puty의 실험결과는 그렇다고 한다). 즉 이윤율이 비대칭하게 분포된다는 거고, 무거운 꼬리를 만든다는거다. 이는 자본의 집중과 집적에 어울릴만한 현상을 보이는 것으로 보이며 이는 "자유경쟁이 독점을 낳는다"는 마르크스-레닌의 태제를 보여주는 것으로 보인다. 다만 아까도 말했으나 이 실험은 완전한 정보를 가정할 수 있다해도 자본이동이 제한적이므로 완전한 자유경쟁의 예로 보기에는 무리가 있을 수 있으므로 확대해석은 금물이다..
참고로 아래에 코드의 플로우차트를 남긴다.
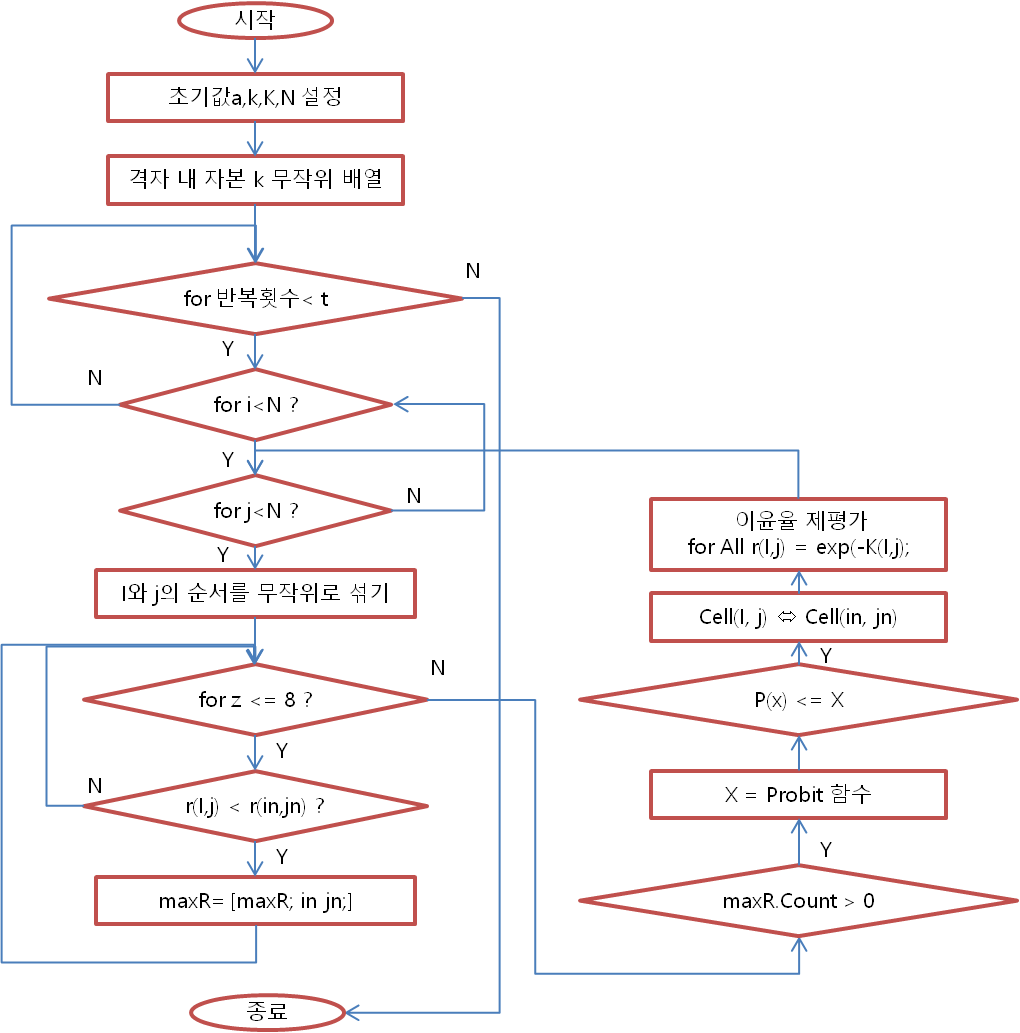
5. 결론
우선 이 결과는 생산가격에 대한 마르크스의 신념에 대해 의구심을 가질만한 결과일 것 같다. 물론 CA의 특성상 이동이 제한적이란 것은 정보에 제한이 있다는 것이고, 물론 이를 반복시행을 무한정 길게 한다면야 문제는 안 되겠지만 이런 특성 상 아담스미스-마르크스의 생산가격 개념을 부정할 수 있다고는 보기 어려울 것 같다. 그럼에도 불구하고 이는 분명 어느정도의 시사를 제공하는 것으로 보인다. 바로 자본 이동은 균등화 과정보다 끊임없이 진동하는 패턴을 보인다는 것이다. 고전적인 틀에서 이를 어떻게 경제학적으로 해석할 수 있을지는 모르겠다. 아니면.. 마경 내에서 소수인 것 같지만 이윤율-잉여가치율 균등화 가정 자체를 부정하는 움직임도 일부 존재한다.
사실 이윤율-잉여가치율 균등화 가정 자체는 분석을 아주 단순하게 해주고 간단하게 해주는 것은 사실이다. 그런데 균등화 가정을 부정한다면? 변수가 늘어나는 것이고 이를 정규화할 방법은 없다. 그러면 이를 해결할 수 있으려면? 이럴 경우는 곧 복잡계의 방법이 그 대안이 될 것이라고 생각된다. 그리고.. 아무래도 그런 추세가 요새 많이 보이는 것 같다. 중요한 것은 이러저러한 연구들을 통합해내는 작업이 언젠가는 필요할 것이라고 생각된다. 세포 자동자를 가지고 프로그래밍하면서 복잡계에 대해 상당한 흥미를 가지게 되었다는 점에서 귀중한 시간이었다. 여러분들도 재밌게 읽어줬으면 좋겠다. 참고로 평소와 다르게 이번에는 코드를 공개하지 않겠다. 이것 때문에 일주일을 개고생했다는 점에서 나름 그 노력에 대해 값어치를 높이려는거다. 쀄애애애액~!
[이관 글. 2016-03-26 작성]
- 이 연구자에 대한 소개 링크. 장관까지 한거 같고 좌파 운동권이었던 듯. http://ultimosegundo.ig.com.br/claudio-puty/53ea375d08ec508e570000a7.html [본문으로]
- Putyy, Claudio Castelo Branco. "A Cellular Automata Model of the General Rate of Profit." Anais do XXXIII Encontro Nacional de Economia [Proceedings of the 33th Brazilian Economics Meeting]. No. 006. ANPEC-Associação Nacional dos Centros de Pósgraduação em Economia [Brazilian Association of Graduate Programs in Economics], 2005. [본문으로]
- 장은성. "복잡성의 과학". p247~354. 전파과학사. 2016. [본문으로]
- 장은성. ibid. p250. [본문으로]
- puty. C. C. B. op. cit. p5. [본문으로]
- puty. C. C. B. ibid. p5. [본문으로]
- puty. C. C. B. ibid. p6. [본문으로]
- puty. C. C. B. ibid. p7. [본문으로]
- puty. C. C. B. ibid. p19. [본문으로]
'정치경제학' 카테고리의 다른 글
| 표준상품과 전형문제 (0) | 2021.05.23 |
|---|---|
| 셸링 모형과 독신자 젠더 거주 모형 (0) | 2021.05.23 |
| 전형문제와 마르코프 연쇄 (0) | 2021.05.23 |
| 환원해법과 FMT (0) | 2021.05.23 |
| 노동가치론의 결합생산 문제 (0) | 2021.05.23 |

