전형문제와 마르코프 연쇄

마르크스는 가치의 생산가격으로의 전형이라는 자신의 해결방식에 대해 "1차적 근사"라는 관점에서 정당화한 바 있다. 즉 계산을 반복하다보면은 목적 해에 근접한 해를 얻을 수 있다고 사고한 것이다. 이러한 아이디어를 수학적으로 표현할 수 있는 것이 마르코프 연쇄에 해당할 것이다. 오늘은 마르코프 연쇄를 통해 이러한 아이디어를 모형화하고 그 의미에 대해 생각해보는 시간을 가질 것이다.

1. 전형문제란 무엇인가

전형문제란 노동가치론의 가치체계를 장기적으로 시장가격이 수렴할 것이라고 가정되는 생산가격을 관련시킬 수 있는 방법이 무엇인지에 대한 것이다. 마르크스는 다음과 같이 생각했을 것은 분명하다.

잉여가치율이 균등하고 단순재생산이 가능한 재생산표식을 가정한다 → 이윤율을 균등하게 구성한다 → 단순재생산에서 성립되었던 관계들을 조정하기 위해 C, V의 괴리율을 비용가격에 곱해서 재전형 → 어라?!! 이윤율의 구성들이 달라졌다! → 이윤율을 균등하게 재구성(끙차끙차) → 어라? 또 비용가격을 재전형 →  ... (반복) ... → 얏호 "정확한" 생산가격에 이르렀다. (이런 방식의 해법을 축자적 해법이라 일컬으며 사이크(1977)^[각주:1]를 참조할 것)

이런 형태는 정확히 마르코프 연쇄와 유사하며 전형문제를 마르코프 연쇄로 풀이하는 시도가 모리시마(1973)로부터 있었다^[각주:2]. 이런 시도는 뭐 당연히 위와 같은 전통적인 해법에 근거한다. 다만 마르코프 연쇄의 가장 좋은 장점은 연립방정식에서 생산가격총계=가치총계 식을 추가하여 푸는 방법이 자의적이며 증명해야 할 것을 전제하고 푼다는 점 등의 비판에 반박할 수 있는 방법이기 때문이다. 즉 마르코프 프로세스로 풀면 생산가격총계=가치총계를 미리 전제하지 않고도 이를 증명할 수 있다는 것이다.

그렇다면 이를 이용하여 정확한 생산가격을 컴퓨터 시뮬레이션을 통해 얻을 수 있지 않을까 생각했다. 게다가 이거 한 번 만들아놓으면 Shaikh(1977) 같은 노가다는 안해도 된다... 예전에 이런 방법을 해보려고 엑셀에다 표만들고 괴리율을 계산하고 또 밑에다 표 만들어서 괴리율 곱해주고 했던 노가다를 생각하면.. (그때 기억으로 엑셀시트에다 한 열 몇 번 해서 생산가격을 얻은 적이 있다만.. 예시가 단순해서 다행이지 한 100번은 해야 얻을 수 있는거였으면 공부고 뭐고 다 때려쳤을지도..) 그래서 이 글이 시작되었다. 덕분에 덕질할 시간을 포기했다.

물론 이렇게 하면 총가치와 총생산가격은 일치하나 총잉여가치와 총이윤은 일치하지 않는다. 하지만 보조적으로 "마르크스의 기본정리"에 따라 이윤율과 잉여가치율의 수학적 관계는 성립됨을 보일 수 있기는 하다. 그러나 더 좋은 전형해법을 찾기 위해 여전히 마르크스경제학은 노력 중이라고 볼 수 밖에 없다. 마르크스의 아이디어는 대강 이랬고 그냥 전통적인 전형해법은 이렇다 하고 넘어가면 될 것 같다.

2. 마르코프 연쇄란 무엇인가

마르코프 연쇄(Markov chain)란 어떤 확률이 그 이전의 확률에만 의존하는 이산적인 과정을 말한다. 이는 어떤 임의의 확률 변수 $X_0,...,X_{n+1}$를 일컬으며, 이들 변수들이 다음과 같은 마르코프 특성을 만족함을 의미한다. ^[각주:3]

$P(X_{n+1}=s_i|X_0=s_j,...,X_n=s_k)=P(X_{n+1}=s_i|X_n=s_k)$

이것이 의미하는 바는 다음 시점의 확률을 예측하기 위해 모든 과거의 확률을 알 필요가 없다는 것을 의미한다. 즉 현재의 확률만 알면 충분하다는 것이고 이것이 마르코프 연쇄의 전제임에 유의하자.

참고로 전형을 풀 때 마르코프 과정(Markov Process)이라고도 하는걸 들었는데. 김달호(2014)를 보니 이는 시점이 이산적이거나 연속적인 경우를 모두 포함한 광의적 의미로 쓰이는 듯 하다. 전형문제를 풀 때는 시간이 이산적이기 때문에 과정이라고 해서 틀린건 아니다만.. 엄밀하게는 마르코프 연쇄라고 명시해야 할 듯 싶어서 이렇게 표현하였다.

3. 마르코프 행렬化

마르코프 연쇄는 그 특성 상 확률변수를 다룬다. 따라서 여가서는 가치든 생산가격이든 확률변수로 가정된다. 합리적인 해석은 가치와 가격모두 확률분포 변수로 가정하는 것이다. 그러므로 각 열 또는 행의 합이 1이 되는 특성을 갖는 마르코프 행렬이 될 수 있다. 먼저 다음의 행렬을 가정하자.

$M=\left[\begin{array}{cc}{A}_1& A_2\\ wb{l}_1& wb{l}_2\end{array}\right]$

$A_1,A_2$는 투입계수행렬을 의미하며, $wb{l}_1,wb{l}_2$는 직접적인 노동투입벡터를 의미한다. 하첨자인 1, 2는 각각 자본재산업$(1,2,...,n)$과 임금재 및 사치재산업$(n+1,..,m)$이 집계되어 있다고 가정한다.

마르코프 연쇄로써 풀기 위해서는 그 특성에 맞는 마르코프 행렬이 필요하다. 즉 각 열 또는 행의 원소의 합이 1인 행렬을 만들 필요가 있다. 이는 다음과 같은 식으로 바꿔주기만 하면 마르코프 행렬이 된다.

$(1+r)M$

각 열의 합계는 투하된 직-간접적 노동과 잉여노동의 합이 되므로 1이 된다. 마르코프 연쇄의 또 다른 특성은 어떤 시점 t의 확률은 t-1의 확률에 의해서만 영향을 받는다는 점에 있다. 따라서 위의 식을 일반적인 마르코프 연쇄 문제로 모형화하면 다음과 같이 된다.

(1) $p_t=p_{t-1}(1+r)M$

마르크스가 생각한 해법을 마르코프 연쇄에 맞게 표현하자면 초기값 $p_0=\lambda$를 이용하여 이윤율 균등화와 비용가격의 재전형이라는 반복계산을 거친 후 더이상 계산이 필요없이 특정한 확률분포로 수렴되는 정확한 생산가격을 얻게 될 것이라고 생각한 것은 분명하다. 따라서 마르코프 연쇄를 반복하여 수렴되는 해(에르고딕 해)가 진정한 생산가격이 될 것이다. 여가서 애르고딕 해란 반복과정을 "이동"이라고 할 때 충분히 큰 "이동"이 일어나는 경우 다음이 성립하는 분포 해를 얻을 수 있다는 것이다.

(2) $p^{\ast }(1+r)M=p^{\ast }$

이 해에 이르게 되면 반복계산은 무의미한데, 왜냐하면 저 특정한 분포확률변수가 더이상 안 바뀌기 때문이다. 그 증명과정은 이 무료서버의 저장공간의 제약으로 여기에 싣지않는다. 페..페르마의 마지막 정리..?!

이 반복계산의 일반적인 계산식을 도출해보도록 하자. 초기의 t=0, 1, 2, ...일 때를 가정하고 (1)식을 풀어 쓰자면 $p_1=p_0(1+r)M,p_2=p_1(1+r)M=p_0\{(1+r)M{\}}^2$. 따라서 이를 일반식으로 나타내면 다음과 같다.

(3) $p_n=p_0((1+r)M{)}^n$

자. 이젠 적절한 마르코프 행렬과 컴푸터가 계산하라고 일시킬 준비(코딩)만 하면 된다.

4. 마르코프 연쇄의 응용

그러면 실제로 계산을 해보자. 마르코프 연쇄를 풀려면 우선 초기값을 정의해야 한다. 우리는 초기값 $p_0=\lambda =\left[\begin{array}{cc}0.5& 0.5\end{array}\right]$과 계산의 편의를 위해 이윤율 $r=0.25$과 총 비용가격 $A+wbl$을 0.8로 가정하여 초기에 시행할 값을 계산해보면 이는 다음과 같다.

$p_0(1+r)M=\lambda (1+r)\left[\begin{array}{cc}{A}_1& wb{l}_1\\ A_2& wb{l}_2\end{array}\right]=\left[\begin{array}{cc}0.5& 0.5\end{array}\right](1+0.25)\left[\begin{array}{cc}0.48& 0.32\\ 0.24& 0.56\end{array}\right]=\left[\begin{array}{cc}0.5& 0.5\end{array}\right]\left[\begin{array}{cc}0.6& 0.4\\ 0.3& 0.7\end{array}\right]$

음.. 이게 위에 예시한 마르코프 행렬이 전치된 듯한 형태가 된 것은.. 음.. 다 이유가 있습니다... 사실 코딩을 저렇게 구성하고 짜버려서임. 고치기 귀찮아 데헿☆

(3)식을 이용하여 반복계산을 시행하고 (2)식이 성립될 때 프로그램이 종료되도록 코드를 설계했다. 컴푸터로 마르코프 연쇄를 시행하여 다음과 같은 해를 얻었다.

$p^{\ast }=\{0.428571...,0.571428...\}$

이렇게 얻은 진정한 생산가격은 가치합계$1=\sum {\lambda }_i$과 생산가격합계$1=\sum p_i^{\ast }$이 일치함을 알 수 있다. 반복계산은 총 30번이 걸렸다.

그래프는 너무 예쁘게 안 나왔는데... 그래도 (와 나 열심히 했다!를 보여주기 위해) 출력.

[그림 1] 전형과정의 p벡터 추이

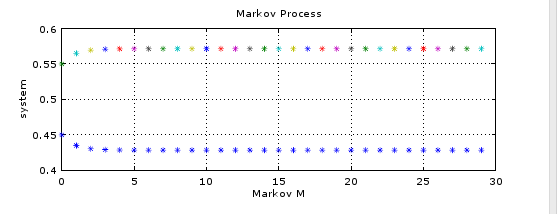
툴은 무료 오픈소스 프로그램인 Octave를 사용하였으며 이 툴이 지원하는 언어는 Mathlab을 기반으로 하였고 (조금의 차이는 있지만) 연동도 가능하다. (아래는 소스코드 링크)

GitHub - azusa0999/MarkovProcess_MarxEconomicTransformation: 마르크스의 전형 과정을 마르코프 프로세스로 푼

5. 결론

다만 이 해법은 아까 말했다시피 마르크스가 생각한 아이디어를 완성한 것이지만 현대 마르크스 경제학에서는 여전히 논쟁적이며, 그냥 해묵은(?) 전통적인 방법에 속한다. 그리고 가치합계와 가격합계가 일치하나 잉여가치합계와 이윤합계는 일치하지는 않는다는 단점이 있다. 보통 이 해법을 옹호하는 측은 마르크스의 기본정리를 보조적으로 이용하여 잉여가치를 이윤과 연관지을 수 있다고 주장한다. 끄읏.

[이관 글. 2015-12-28 작성]

1. Shaikh, A. (1977). Marx’s theory of value and the transformation problem. The subtle anatomy of capitalism, 106-37. [본문으로]
2. Morishima, M. (1973). Marx's economics: a dual theory of value and growth. CUP Archive. 국역본. "맑스의 경제학-가치와 성장의 이중이론. p132 주석 (5), (6) 참고. 류동민 (역). 나남출판사. 2010. [본문으로]
3. 김달호. (2014). 몬테칼로 통계계산. p175. 자유아카데미. [본문으로]