티스토리 뷰
서론
이전의 글 [시점간 체계에 대한 보론 - 시뮬레이션]에서, 나는 시점간 체계가 기술적 조건과 노동량이 고정되었을 때 무한대로 가면 동시적 체계로 수렴하는 것을 보였다. 하지만 시뮬레이션을 해보면 시점간 체계는 무척 빠르게 동시적 체계로 수렴한다는 것을 알 수 있었다.
그러나 진정한 시점간 체계는 기술적 조건과 노동량이 변한다고 가정한다. 예컨대 Mohun(2009)1을 보면 $A$와 $l$에 시점을 표현하지 않았으나 산출량벡터 $x$에 하첨자 $t$를 표현하고 있다는 사실을 보면, 산출량벡터가 결국 투입계수행렬 $A$를 구성하기 때문에 당연히 $A$는 생산이 완료된 시점으로 표현되는 것이 맞다. 또한 Kliman(1999)2은 $A$와 $l$에 시점 $t$를 표현하고 있지 않는 것으로 보이는데, 이는 쉽게 설명하기 위한 대책일지 모르나 엄밀한 의미에서 우리가 시뮬레이션을 통해 알게 되었듯이 무한대가 아니라 동시적 체계로 매우 "빠르게" 수렴한다는 것을 알게 된 이상 이는 주지해야 할 것이다. 다른 예로 김창근(2005)3의 경우 $A$와 $l$에 시점을 표기한 바 있다.
따라서 우리는 $A$와 $l$에 시점을 표기한 경우가 시점간 체계(TSSI)의 예에 더 적합한 형태라는 것을 알 수 있게 되었다. 즉 이 둘은 고정되는 것이 아니라 변한다는 사실이고 시점간 체계는 일반적으로 이를 가정하고 있다는 것이다.
수학적 접근
이제 우리는 다음과 같은 체계를 보일 수 있다.
$\lambda_{t}=\lambda_{t-1}A_{t}+l_{t}$
$t$ 시점의 기술적 조건과 노동량은 이전의 구매된 가치 $\lambda_{t-1}$로 평가되는 것이다. 이 체계의 초기값을 $p_{0}=\lambda_{0}$라고 하고 차분방정식을 풀어보자. 먼저 초기값에 의해 주어지는 첫 번째 시점의 가치는 다음과 같이 정의된다.
(1) $\lambda_{1}=p_{0}A_{1}+l_{1}$
다음 시점에는
(2) $\lambda_{2}=\lambda_{1}A_{2}+l_{2}$
우변의 앞에 항에 $\lambda_{1}$을 (1)식과 같으므로
$\lambda_{2}=(p_{0}A_{1}+l_{1})A_{2}+l_{2}$
이를 전개하면
$\lambda_{2}=p_{0}A_{1}A_{2}+l_{1}A_{2}+l_{2}$
이제 $t=n$ 개의 시점으로 확장하면 다음과 같은 일반적인 식을 얻는다.
(3) $\lambda_{t}=p_{0}A_{1}A_{2}...A_{n}+l_{1}A_{2}...A_{n}+l_{2}A_{3}...A_{n}+...+l_{n-1}A_{n}+l_{n}$
만약 $n>2$라고 한다면 다음과 같이 축약할 수 있다.
$\lambda_{n}=p_{0}\prod_{j=1}^{n}A_{j}+\sum_{i=1}^{n-1}\prod_{j=i+1}^{n-i}l_{i}A_{j}+l_{n}$
이제 이것이 무한대로 간다고 하자.
$\lim_{n\to{\infty}}p_{0}\prod_{j=1}^{n}A_{j}+\sum_{i=1}^{n-1}\prod_{j=i+1}^{n-i}l_{i}A_{j}+l_{n}$
여기서 우변의 앞 항 $p_{0}\prod_{j=1}^{n}A_{j}$은 레온트에프 행렬의 원소가 모두 $0\leq{a_{ij}}<1$이므로 0으로 수렴하게 되어 소거된다.
(4) $\lim_{n\to{\infty}}\sum_{i=1}^{n-1}\prod_{j=i+1}^{n-i}l_{i}A_{j}+l_{n}$
그러나 남은 뒤의 항은 어떻게 될까. 그것은 수렴하지 않고 발산할 것이라고 본다. 이를 증명하기 위해 귀류법을 사용해보자. 예컨대 (4)식의 앞 항이 너무너무너무 방대하게 큰 수 $m$로 무한히 접근할 때, 어떤 실수 $d$로 수렴한다고 먼저 가정해보는 것이다. 이제 그 이후는 더 이상 나아가지 못한다는 거다.
(5) $\lim_{n\to{m}}\sum_{i=1}^{n-1}\prod_{j=i+1}^{n-i}l_{i}A_{j}=d$
이제 $m+1$로 무한히 접근하면 수렴하는 $h$가 있다고 하자.
(6) $\lim_{n\to{m+1}}\sum_{i=1}^{n-1}\prod_{j=i+1}^{n-i}l_{i}A_{j}=h$
그런데 이는 $d$로 수렴한다는 전제와 모순된다. 따라서 (4)식은 발산한다.
16.10.20 추가적인 증명사항
왠지 부족함이 느껴져서 추가적인 보완을 하고자 한다.. (수알못이라 죄송합니다) 먼저 $d-h$를 한다고 하면
$d-h=l_{1}A_{2}...A_{m}(I-A_{m+1})+...+l_{m-1}A_{m}(I-A_{m+1})+l_{m+1}$
$=(l_{1}A_{2}...A_{m}+...+l_{m-1}A_{m})(I-A_{m+1})+l_{m+1}$
물론 $d$와 $h$는 극한에 의한 가상의 결과라고 가정하고 있는데, 물론 극한으로 설정하지 않아도 앞에 $p_{0}A_{1}...A_{n}$은 공통항이므로 소거된다. 이제 만약 (5)에서 수렴한다면 다음이 성립함을 보여야 한다.
$(l_{1}A_{2}...A_{m}+...+l_{m-1}A_{m})(I-A_{m+1})+l_{m+1}=0$
이는 모든 $i$에서 직접노동량 $l_{i}>0$이라는 노동가치론의 전제에 의해 앞의 항 $(l_{1}A_{2}...A_{m}+...+l_{m-1}A_{m})(I-A_{m+1})$이 $l_{m+1}$의 역원이어야 함을 알 수 있다. 여기서 역원이라 함은 "덧셈의 역원"이므로 $(-1)l_{m+1}$과 $(l_{1}A_{2}...A_{m}+...+l_{m-1}A_{m})(I-A_{m+1})$이 같아야 한다는 거다.
그러나 투입계수행렬 $A$는 생산적이다. 즉 모든 $i$에서 $(I-A_{m+1})>0$은 언제나 성립한다.
그러므로 $l_{1}A_{2}...A_{m}+...+l_{m-1}A_{m}$의 결과가 음(-)이어야 하는데, 이는 $l_{i}>0$이라는 가정과 투입계수행렬 $A$는 생산적이라는 가정과 모순된다.
따라서 (4)식은 발산한다.
시뮬레이션
이제 시뮬레이션을 진행해보자. 나는 이미 이전의 글 [시점간 체계에 대한 보론 - 시뮬레이션]에서 호킨스-사이먼 조건이 성립하는 투입계수행렬을 랜덤하게 던져주는 모듈을 개발한 바 있다. 이것을 이용하여 $A$를 매 시점마다 랜덤하게 얻어 시점간 과정을 반복해서 그 추세를 확인해보도록 하자.
나는 가치벡터의 초기값 [21, 37]로 12만 번의 횟수로 시행해보았다. 아래 [그림 1]은 그 결과이다.
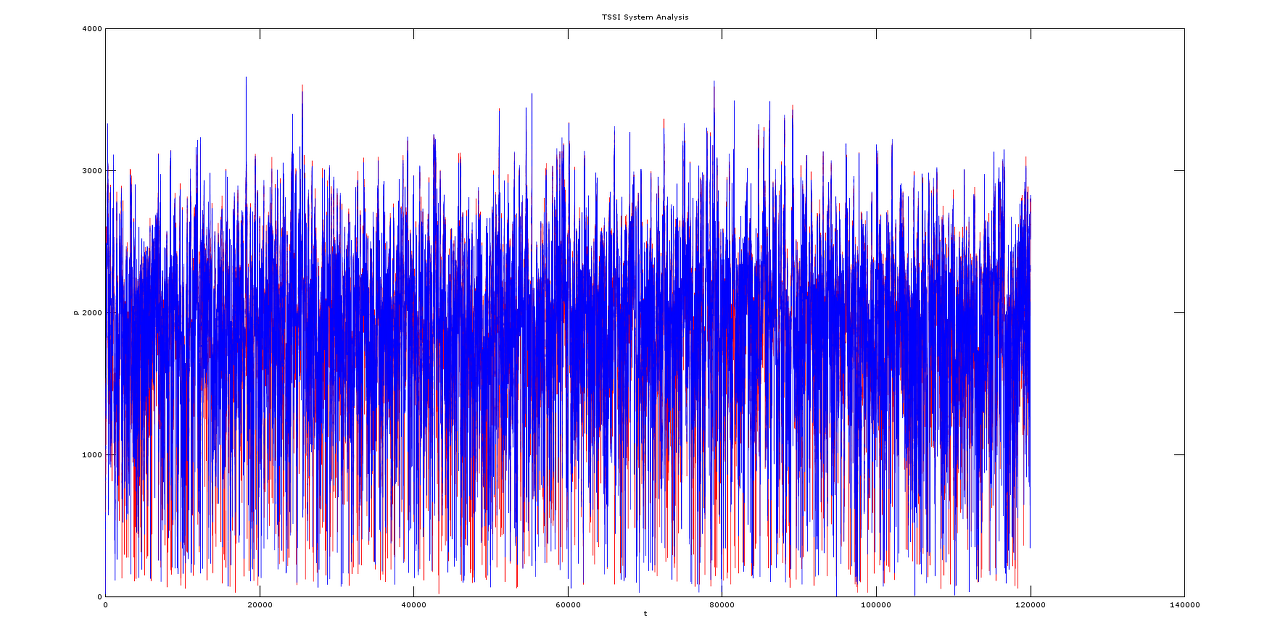
12만 번의 시행에도 불구하고 두 개의 가치변수는 무한정 흔들리는 패턴을 보이고 있다. 시뮬레이션의 시행결과 역시 시점간 체계에 부정적인 의미를 보이고 있음을 알 수 있다.
결론
우리가 지금까지 확인한 바는 다음과 같다.
- 시점간 체계에서 기술적 조건과 노동량을 고정할 때, 시뮬레이션을 시행하면, 그것은 매우 빠르게 동시적 체계로 수렴한다.
- 시점간 체계에서 기술적 조건과 노동량이 매 시점마다 변한다고 가정한다면 발산한다.
지금까지의 결과를 통해 이것은 무엇을 의미하는지 음미해보자.
- 시점간 체계 모형은 기술적 조건과 노동량을 고정시키는 가정을 하면 안 된다. 시뮬레이션의 결과는 그것이 매우 빠르게 동시적 체계로 접근한다는 것을 알 수 있다. 따라서 그것은 시점간 체계 이론의 고유성을 깨뜨릴 것이다.
- 시점간 체계는 매 시점마다 기술적 조건과 노동량이 변동한다고 가정하는 것이 일반적인 것이라고 생각한다. 이럴 경우 우리의 시뮬레이션은 그것이 발산한다는 것을 보였다. 이 말은 모형 자체가 불완전하다는 것이다.
- 물론 시점간 체계는 균형이라는 개념에 대해 완강히 거부한다. 4 따라서 발산의 문제는 이들에게 큰 문제가 아닐 수도 있다. "자본주의는 일반균형이 내포하는 정태적인 체계가 아니라 끊임없이 '운동하는’ 경제체계이기 때문이다. 오히려 신리카도학파와 같이 일반균형에 매몰되면, 자본주의의 본성을 올바르게 이해하지 못하게 된다."5
- 물론 균형에 대한 그들의 생각에 나는 부정적이다. 마경 내에는 균형에 대한 개념들이 서로간에 논쟁적인 주제이긴 하다. 예컨대 Sekine(2003)6는 시점간 체계의 균형개념 거부에 대해 비판하며 "일반균형으로의 경향을 인정하지 않는다면 그 경제는 자본주의라고 할 수 없다"고 비판했다. 하지만 시점간 단일체계가 신리카디언의 모형(즉 스라파 모형)을 왈라스적 모형이라고 하는 데에는 오해라고 본다. 예컨대 롱칼리아(1978)7의 경우 스라파 모형은 경제의 운동과정의 스냅사진과 같은 것이라고 해석했다. (이것 역시 스라파경제학 내에서는 논쟁적이라고 언급하긴 했다) 즉 특별히 신리카도주의가 균형 개념을 필요로 하지 않는 해석이 가능하다는 점에서 언급하고 지나가겠다.
- 그러나, 이들이 균형개념을 필요로 하지 않는다고 하더라도 현실적으로 발산하는 경제가 현실적이라고 말하려면 좀 더 충분한 실증근거가 뒷받침되어야 할 것 같다. 자본주의는 물론 대체로 불완전하긴 하다. 이것을 부정하진 않는다. 그러나 그렇다고 해서 그 불완전함을 모형에 재현했다고 말하는 것은 곤란하며 아무 상관이 없는 것이다.
[이관 글. 2016-10-17 작성]
- Mohun, Simon, and Roberto Veneziani. "The Temporal Single-System Interpretation.". pp280. 마르크스주의 연구 6.3 (2009): 277-301. [본문으로]
- Kliman, Andrew J., and Ted McGlone. "A temporal single-system interpretation of Marx's value theory." Review of Political Economy 11.1 (1999): 33-59. [본문으로]
- 김창근. "맑스의 가치론과 시간 : 시점간 단일체계 해석의 확장". p96. 서울대학교 대학원 박사학위논문.2005. [본문으로]
- Carchedi, Guglielmo. "The logic of prices as values∗." Economy and Society13.4 (1984): 431-455. [본문으로]
- 김창근. 2005. op. cit. p123~124의 주석 120 참고. [본문으로]
- Sekine, Thomas T. "Marxian Theory of Value, What We Might Learn from It.". p7. Korean journal of Political Economy 2 (2004): 1-35. [본문으로]
- Roncaglia, Alessandro, and Jan Allen Kregel. "Sraffa and the Theory of Prices". New York: Wiley, 1978.<번역본>스라파와 가격이론. 박만섭 역. [본문으로]
'정치경제학' 카테고리의 다른 글
| 이윤율 역수는 왜 투입계수행렬의 고유값인가 (0) | 2021.05.23 |
|---|---|
| 뒤메닐이 언급한 왈라스의 실수에 대한 노트 (0) | 2021.05.23 |
| 시점간 체계에 대한 보론 -시뮬레이션 (0) | 2021.05.23 |
| 시점간 체계의 발산문제 (0) | 2021.05.23 |
| 선형생산모형과 노동생산성에 대하여 (0) | 2021.05.23 |
