티스토리 뷰
마르크스 경제학은 가치의 실체가 노동이라고 본다. 그러므로 그 양적 정의도 노동량이 된다. 따라서 어떤 상품에 응고된 가치량은 노동량이 된다. 그런데 생산과정을 좀 더 생각해보자. 어떤 한 생산과정이 이루어진다면 단 하나의 상품만을 생산하는 것이 일반적인 것인가? 마르크스의 자본론 1권도 모두 그런 가정을 암묵적으로 전제하고 있다. 그렇게 생각하면 "어떤 상품이 생산되는데 사회적으로 필요한 노동량"이라는 개념은 아무런 문제가 없다. 그런데 어떤 상품을 생산하는 노동이 행해질 때 동시에 다른 n개의 상품이 생산된다고 하자. 그렇다면 이 상품에 응고된 노동량은 같을 것이다..... 어라. 잠깐만. 그럴리가 없잖은가.
예를 들어 목재를 가공하는 생산과정에서 톱밥이 생산되며 이는 목판을 만드는 원재료로써 사용될 것이므로 이 역시 노동이 응고된 가치를 가질 것이다. 그러면 생산된 목재의 가치와 톱밥의 가치는 동일해야 하는데 과연 이렇게 말할 수 있을까. 일단 같다고 말할 수 있다고 하더라도 그게 진짜 문제는 아니다. 진짜 문제는 결합생산물을 가정하게 될 때 첫째. 양(+)/0/음(-)의 이윤이 존재한다면 양(+)/0/음(-)의 잉여가치가 존재한다는 마르크스의 기본정리(이하 FMT)가 성립하지 않을 수 있다. 둘째. 결합생산물을 가정할 경우 생산가격이 존재하지 않을 수가 있다. 생산가격이 존재하지 않는다면 노동가치론의 추상수준을 낮추는 중요한 방법론 하나가 파괴되는 것이다. 이것이 사실이면 마르크스 경제학에 파괴적인 영향을 끼치는 것은 당연하다.
이렇듯 생산과정에서 동시에 두 가지 이상의 상품이 생산되는 경우를 "결합생산 結合生産 Joint Production"이라고 한다. 피에로 스라파는 자본이란 개념을 생산과정에서 감가되면서도 낡은 기계를 생산하는 결합생산물로 볼 것을 제안하기도 하였다1. 스라파의 예를 생각해보면 결합생산의 예는 이론적 가상으로 정립할 수 있고 또한 현실에서도 이와 같은 경우를 찾기는 쉽다. 다음과 같은 경우가 현실의 예일 것이다.
- 목재와 톱밥
- 우유와 쇠고기
- 계란과 닭고기
- 양모와 양고기
- 제분공장, 설탕공장 등과 공해(공해가 생산된다)
- 비행기/철도 교통과 화물운송
이렇듯 노동가치론의 입장에서 이론의 "일반화"를 원한다면 하나의 생산과정이 하나의 상품을 생산한다는 가정이 아니라 n개의 상품이 생산되는 경우까지 모두 설명되어야 할 것이다. 왜 그래야하는가? 왜냐하면 현실이 그렇게 작동하는 경우가 흔하게 존재하니까. 생산과정을 중시하는 노동가치론이 이런 생산과정에 대해서만은 설명을 회피할 정당한 이유가 있을까.
어찌되었든 결합생산의 문제는 마르크스 경제학이 전제하는 노동가치론에 골치아픈 문제를 안겨주었다. 게다가 대중적인 지점에서 이 문제의 심각성이 전형 문제보다 제대로 전파되지 못했다는 것을 본 필자는 충분히 인지하고 있다.
이 글은 다음과 같이 진행할 것이다. 우선 스티드먼의 FMT에 대해 알아본다. 스티드먼은 결합생산물을 도입하게 되면 FMT가 적용되지 않는다고 한다. 즉 이윤이 양인데 잉여가치는 음인 상황이 될 수 있다는 것이다. 그 다음 이에 대한 논쟁사를 간단히 요약하고, 마지막으로 결합생산물을 가정할 시 생산가격이 존재하지 않을 수 있다는 점에 대해 알아본다.
스티드먼의 결합생산물과 FMT
스티드먼(1975)2은 하나의 생산과정은 하나의 상품만을 생산한다는 가정을 제거하고 결합생산물을 용인하게 되면 FMT가 성립되지 않는다는 것을 입증하였다. 그러니까 이윤이 양(+)인데 잉여가치는 음(-)인 상황이 존재한다는 것이다. 다음의 [표1]은 스티드먼의 예를 보여주는 것이다.
[표 1] 3
| 상품 1 | 상품2 | 노동 | 상품1 | 상품2 | |||||||||
| 과정 1 | 5 | + | 0 | + | 1 | → | 6 | + | 1 | ||||
| 과정 2 | 0 | + | 10 | + | 1 | → | 3 | + | 12 | ||||
이 표를 생산가격 방정식으로 나타내면 다음과 같다.
(1) $(1+r)5p_1+1=6p_1+p_2$
(2) $(1+r)10p_2+1=3p_1+12p_2$
생산가격 방정식을 보면 이윤율 $r$이 자본투입계수에서만 곱해져 있는 형태를 볼 수 있는데, 마르크스 경제학에서는 보통 총투입자본에 대해 이윤율을 곱해야 하기 때문에 뭔가 다르다. 이에 대해 알아보니 이는 스라파의 해석에 기초한 것이라고 한다4. (16.6.6 추가 : 스라파는 노동자에게 필수재의 형태로 임금이 선불됨과 동시에 그것을 초과하는 잉여생산물이 존재하게 되는데. 이때 자본가와 노동자가 나눠갖는 임금후불을 가정한다. 따라서 (1)식의 가정은 보통 임금후불 모델이라 할 수 있으나 물론 필수재의 형태는 선불된다는 점에서 복합적이다) 마르크스 경제학 내에서도 이에 대해 특별한 지적을 하지 않는 것으로 보아 그 결론에 큰 문제가 아닌 것 같다. 어찌되었든 노동자가 받는 임금을 $1/2$ 단위의 상품 1과 $5/6$ 단위의 상품 2를 받는다고 가정하면 실질임금은 아래와 같이 정의된다.
(3) $3p_1+5p_2=6$
그러면 3개의 미지수에 대한 3개의 식이므로 해를 풀 수 있다. 따라서 미지수는.
$r=+20\%,p_1=\frac{1}{3},p_2=1$
여기까지는 정상적으로 보인다. 그러면 다른 한편으로 가치 방정식으로 [표1]을 나타내보자.
$5\lambda_1+1=6\lambda_1+\lambda_2$
$10\lambda_2+1=3\lambda_1+12\lambda_2$
그러면 해는 $\lambda_1=-1,\lambda_2=2$가 된다. 어라? 뭔가 이상한게 지나간 거 같은데.. 다음으로 노동력의 가치를 V, 잉여가치를 S라고 하면.
$V=3\lambda_1+5\lambda_2=3\times(-1)+5\times2=7$
$S=5\lambda_1+2\lambda_2=5\times(-1)+2\times2=-1$
$V+S=6$
그러므로 이윤율 $r(=20\%)$은 양(+)인데 잉여가치 $S(=-1)$는 음(-)이 되어 FMT가 성립하지 않는다. 그리고 음(-)의 가치 $\lambda=-1$가 발생한다....라는 놀라운 결과가 발생한다5. 결합생산물 세카이헤 요우코소!
왜 음의 잉여가치가 발생하는가
이에 대한 흥미로운 지적이 울프스테터(1976)6로부터 나온 바 있다. 즉 생산과정 1이 생산과정 2에 비하여 생산성이 절대적으로 열등하기 때문이라는 지적이다. 따라서 뭐가 문제겠는가. 바로 (1)과 (2)식에서 모두 동일한 이윤율 r을 사용하면 안 된다는 것이다. 생산성이 크게 차이가 나는데 동일한 이윤율을 가정하는 것은 자본들 간의 자유로운 경쟁이라는 가정과도 모순된다는 지적이다7.
다른 한편으로 기술변화 Technical Change 문제에 대한 것이다. 먼저 동일 부문 내에서 급격한 기술혁신이 일어났다고 가정해보자. 그렇게 된다면 신-기술을 채택한 기업과 구-기술을 유지하는 기업이 존재하게 되고 생산성의 격차가 발생한다. 마르크스는 이러한 상황을 개별가치와 사회적 가치의 구분을 통해 설명하려고 시도한다.
따라서 만약 새로운 방법을 채용하는 자본가가 자기의 상품을 12원이라는 사회적 가치로 판매한다면, 그는 그 상품을 개별 가치보다 3원 더 비싸게 판매하는 것으로 되며, 따라서 3원의 특별잉여가치(特別剩餘價値: extra surplus-value)를 실현하게 된다. (...) 기타의 조건이 같다면, 그의 상품은 오직 가격인하(價格引下)를 통해서만 시장을 확대할 수 있다. 그러므로 자본가는 상품을 그 개별 가치보다는 비싸게, 그러나 그 사회적 가치보다는 싸게, 예컨대 1개당 10원에 판매할 것이다.8
그러니까... 스티드먼은 개별가치와 사회적가치를 구분하지 않았기 때문에 생산성 격차가 발생하는 시점에 대해서만 사용한다고 볼 수 있으므로 그 해가 음(-)이 된다는 것이며 이런 관점에서 비판이 이루어지기도 하였다9. 그런데 이런 경우 결합생산물을 가정할 때 두 가지 이상의 상품에 대한 개별가치를 확정할 수 있는가에 대해 추가적인 문제가 밝혀졌고 이에 대한 기술적인 문제들이 논의되어왔다1011.
결론적으로 말하자면 결합생산물을 가정할 경우 개별가치를 구하는 것은 불가능하다. 이것은 어찌보면 당연하다. 마르크스 경제학이 사용하는 단일생산물 방정식에서 두 가지 이상의 미지수가 추가되게 되고, 그에 해당하는 추가적인 식을 나타낼 방법을 찾을 길이 없기때문이다. 물론 그런 적절한 방법을 잘 찾는다면 문제를 풀 수 있겠으나.. 글쎄 잘 모르겠다. 해결이 된다면 적어도 캠브릿지 저널에 논문을 실어줄만한 이슈가 아닐까하는 개인적인 생각. 결론적으로 결합생산물이 존재할 때 개별가치를 확정하기 어렵다는 사실을 인정해야만 한다. 따라서 이런 관점으로 스티드먼을 공격하는 것은 유효하지 못했다고 개인적으로 평가된다. 게다가 이걸 그냥 넘어가기는 어려울만큼 더 큰 문제가 발생하는데 개별가치와 사회적 가치라는 구분이 과연 결합생산물을 인정하는 일반화된 가정 속에 위치시킬 때 유효한가에 대한 의심까지 덧붙여지게 된다. 즉 스티드먼의 비판은 아직도 유효하게 마르크스 경제학에 골치를 안겨주고 있다.
이윤율 균등화조건과 결합생산물
위에서 처음에 언급한 생산성 격차와 이윤율 균등화 조건이 양립할 수 없다는 것에 대해 먼저 지적한 바가 있다. 그렇게 된다면 다음의 결론을 내고도 남는다.
- 이윤율 균등화 조건을 전제하는 생산가격은 단일생산물 모형에서만 유효하다.
- 따라서 결합생산물 모형에서는 생산가격이 존재하지 않는다(?)
그래서 문제가 무엇일까? 바로 이윤율 균등화 조건 때문이다. 생산성의 격차가 존재함에도 이윤율 균등화 가정이 정당한가의 문제는 이미 위에서 살펴본 결합생산물 모형에서 확실해진 것으로 보인다.
그렇다면 단일생산물모형에서도 생산성 격차가 존재한다면? 이런 경우는 문제가 안 될 수 있다. 자본 이동이 이윤율 균등화를 낳는 것이지 서로 다른 부문 간에 생산성 격차가 자본 이동에 영향을 끼칠 것 같지는 않다. 예를 들어 전기산업과 신발산업 간에 생산성 격차가 자본이동을 가로막는가? 그렇진 않다는 것이다. 다만 결합생산물을 가정할 때는 생산성 격차가 문제가 된다. 하나의 기업에서 두 가지 이상의 상품이 동시에 생산되는데 기업 안에서 자본이동을 할 리도 없고 이 생산과정이 동일한 이윤율을 낳을 매커니즘을 가정하기도 어려워보인다. 어찌되었든 그렇다면 모형의 일반화라는 측면에서 이윤율 균등화 조건은 일종의 단순화 가정에 불과하며 일반화된 모형에서는 "제거되어야 할" 가정이 되는 것이다.
참고로 스라파의 표준상품생산체계의 경우는 어떨까? 그들의 연립방정식 체계는 상대가격과 분배변수가 동시에 결정되기 때문에 거기에 더해 수요의 변화까지 고려하더라도 생산가격의 존재성에 문제가 없다는 것이 입증되었다12. 표준상품이 역시 최거시다
이 문제에 대한 해법에 있어서 폴리(1985)13의 논의를 먼저 살펴보도록 하자. 원문을 읽을 재간이 거의 없는 필자라서;;; 두 사람의 논의를 정리한 류동민(1994)14의 논의를 참고해보도록 하자.
폴리는 두 개의 재화와 두 개의 생산과정이 존재하는 경우를 고려하였다. 단 $b_1,b_2$는 상품 1, 2의 생산량이며 이윤율 $r$을 얻는 생산과정은 $p_1b_1+p_2b_2=(1+r)(p_1a_1+p_2a_2+l_u)$로 표시된다.
따라서 다음의 부등식을 만족시키는 $p_1,p_2$는 이 생산과정을 통해 $r$ 이하의 이윤율을 얻는 가격수준의 집합이 바로 "생산가격"이 되는 것이다.
(4) $p_2\leq\frac{(1+r)l_u-p_1[b_1-(1+r)a_1]}{[b_2-(1+r)a_2]}$
(4)식을 $(p_1,p_2)$로 이루어진 2차원 평면에 나타낸다면 단일생산물 모형에서는 직선의 기울기는 $b_1-(1+r)a_1$과 $b_2-(1+r)a_2$의 부호에 따라 결정될 것이다. 그런데 결합생산물 모형에서는 두 변수가 모두 양의 부호를 갖는다. 왜냐하면 두 식은 투입물을 단순히 보전할 뿐만 아니라 일정한 율($r$)로 이윤을 분배한 뒤에도 순생산물이 남는다는 것을 의미하기 때문이다15. 따라서 적어도 하나의 생산과정에서 (4)식은 기울기가 음이 된다.
아래의 그림16에서 <그림1>과 <그림2>의 경우는 균등한 양(+)의 이윤율을 담보하는 양(+)의 가격체계 p*가 존재함을 알 수 있다. <그림1>의 경우는 하나의 생산과정만 결합생산인 경우이며, <그림2>의 경우는 두 과정 모두 결합생산인 경우를 보여준다.


다음으로 <그림3>과 <그림4>의 경우는 위의 경우와 같이 하나의 과정만이 결합생산물, 두 개의 과정 모두 결합생산물인 경우이나 음(-)의 가격체계가 존재하는 경우이다.

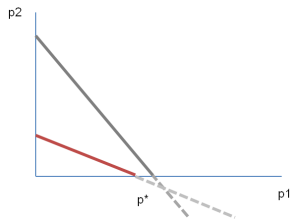
이 직선의 붉은 선으로 표현된 직선의 범위 안에서는 하나의 과정은 r의 이윤율을 얻으며 다른 과정은 $r$ 미만의 이윤율을 얻는 양(+)의 가격체계 집합이 된다. 현실에서 $p*$와 같은 음(-)의 가격체계는 존재하지 않으므로 이 범위 안에서 가격이 결정될 것이다. 폴리는 이 붉은 직선 상에서 양(+)의 이윤을 보장하는 가격집합을 생산가격으로 파악하자고 제안한다.
이후 이 결과는 마나라(1980)17, 뒤메닐&레비(1987)18에 의하여 이것이 수학적으로 일반화 되었다.
$M(r)=B-(1+r)A$로 정의되는 $r$-순생산물(r-net output) 개념을 이용하면 양의 생산가격이 존재하기 위한 필요충분조건이 다음과 같은 두 가지 조건이 성립되어야 함을 증명할 수 있다.
첫째. $ZM(r)=Z[B-(1+r)A]\leq0$인 양의 벡터 $Z$가 존재하지 않는다.
둘째. $ZL\geq{Z'L}$이고 $ZM(r)=Z[B-(1+r)A]\leq{Z'M(r)}=Z'[B-(1+r)A]$인 양의 벡터 $Z,Z'$가 존재하지 않는다. 일단 뭔소린지 모르겠지만 맞겠지 뭐
이것의 경제적 의미는 다음과 같다. 첫 번째 조건은 투입물을 단순히 보전할 뿐만 아니라 일정한 율(r)로 이윤을 분배한 뒤에도 남는 순생산물이 최소한 하나의 상품에 대해서는 양이어야 한다는 것을 의미한다. 두 번째 조건은 노동투입량이 더 많음에도 불구하고 이러한 의미의 순생산이 더 적어서는 안 된다는 것이다.
이해를 돕고자(나도 나를 돕는다) 류동민(1994)은 이 필요충분조건을 스티드먼의 예에 적용하는데 이 예를 살펴보자. 스티드만의 예에서는 이윤율 $r$이 $20\%$이다. 따라서 생산가격이 존재할 것이다. 왜 존재하는지 이 필요충분조건으로 검증할 수 있다. 스티드먼의 예는 그러므로 두 가지의 조건이 충족될 것임은 분명하다. 임의의 $Z'=(z_1,z_2)$에 대해 $ZL=6>Z'L=z_1+z_2$라면, $ZM(0.2)=(3,5)<Z'M(0,2)=(3z_1,z_2)$의 조건은 성립하지 않는다. 후자가 성립되기 위해서는 $z_1>1$이고 $z_2>5$이어야 하는데 그렇다면 $z_1+z_2<6$일 수가 없기 때문이다.[Q.E.D]
결론
그런데 생산가격을 저렇게 개념화 하면 생산가격은 더 이상 시장가격의 규제자라는 개념으로 설명할 수는 없게 되는 난점이 제기되기도 한다. 그냥 어떤 양의 이윤율을 담보하는 생산가격의 집합 중에 결정되는 방식이 되어버리기 때문이다(음.. 시장가격은 저 가격집합 중에 마음에 드는 것 주위를 맴돌거예요). 이 부분에 대한 방법론적 해소는 새해석의 방식처럼 가격변수와 분배변수를 "주어진 것으로" 가정하면 쉽게 해결되는 문제일 수도 있다. 다만 나는 이게 뭔가 좀.. 아름답지 않아 보인다. 그렇다해도 프리드만이 예전에 얘기했듯이 까짓꺼 현실설명만 잘 되면 그게 좋은 이론인거야! 라고는 할 수 있겠지만.. 아직 잘 모르겠다.
또 하나의 문제로는 결합생산물 모형에서 가치량을 확정할 수 있느냐가 문제이다. 이 문제는 안타깝게도 아직 난제인 상황이다. 그냥 개인적인 생각으로는 우리가 여기까지는 왔다는 생각이 든다. 아직 멀었지만 뭔가가 보이는 느낌. 아.. 그런데 왜이리 깜깜하지?!
[이관 글. 2015-11-29 작성]
- Sraffa, P. (1975). Production of commodities by means of commodities: Prelude to a critique of economic theory. CUP Archive. [본문으로]
- Steedman, I. (1975). Positive profits with negative surplus value. The Economic Journal, 114-123. [본문으로]
- Steedman, I. (1975). ibid. p115. [본문으로]
- 이채언. (1992). 경제학에 있어서 가치와 가격. 경영논총 제 17집. pp51-70. [본문으로]
- Steedman, I. (1975). op. cit. p116. [본문으로]
- Wolfstetter, E. (1976). Positive profits with negative surplus value: a comment.The Economic Journal, 864-872. [본문으로]
- Farjoun, E. (1984) 'Production of commodities by means of what?' In E. Mandel and A. Freeman (eds.), Ricardo, Marx, Sraffa, London: Verso. [본문으로]
- Marx, K. (2001). 자본론 I (상). p429~430. 김수행 옮김. 제 2 개역판. 비봉출판사. [본문으로]
- Savran, S. (1984). The Negation of Negative Values. Ricardo, Marx, Sraffa, London: Verso. [본문으로]
- Armstrong, P., Glyn, A., & Harrison, J. (1978). In Defence of Value a Reply to Ian Steedman. Capital & Class, 2(2), 1-31. [본문으로]
- Stamatis, G. (1983). On Negative Labor Values. Review of Radical Political Economics, 15(4), 81-91. [본문으로]
- Schefold, B. (1985). On changes in the composition of output. Political economy, 1(2), 105-142. [본문으로]
- Foley, D. K. (1985). On prices of production in a general model of production.Contributions to Political Economy, 4(1), 25-36. [본문으로]
- 류동민. (1994). 가치이론의 정합성과 분석적 의의에 관한 연구. p48. 서울대 경제학과 박사논문. [본문으로]
- 류동민. (1994). ibid. p48-49. [본문으로]
- 류동민. (1994). ibid. p49. [본문으로]
- Manara, C. F. (1980). Sraffa's model for the joint production of commodities by means of commodities. Essays on the theory of joint production. [본문으로]
- Duménil, G., & Lévy, D. (1987). Value and natural prices trapped in joint production pitfalls. Journal of Economics, 47(1), 15-46. [본문으로]
'정치경제학' 카테고리의 다른 글
| 전형문제와 마르코프 연쇄 (0) | 2021.05.23 |
|---|---|
| 환원해법과 FMT (0) | 2021.05.23 |
| 환원해법에 대한 방법론적 고찰 (0) | 2021.05.23 |
| 경제계산논쟁과 향후 계획경제의 시사점 (2) | 2021.05.23 |
| 정보재 가치 논쟁과 독점-지대설 (0) | 2021.05.23 |

