티스토리 뷰
이 분석을 해보는 이유는 노동시간의 화폐적 표현 MELT가 새해석의 말대로 순부가가치에 대해 얼마나 그 관계가 안정적인가에 대한 의문에서 시작되었다. 순부가가치에 대한 상대적 안정성이란 순부가가치와 MELT가 상관관계가 높아야 한다는 것을 의미한다.
이에 따라 오랜만에 회귀분석도 공부해볼 겸, 겸사겸사 간단한 회귀분석을 시행해보고자 했다.
데이터의 수집방법
먼저 순부가가치는 국민계정에서 국민총소득 GNI에서 고정자본소모율을 곱한 값을 뺀 것으로 정의할 수 있다.
$NNI=GNI(1-c)$ (c는 고정자본소모율이다)
(이게 새해석에 부합하는 정의인지는 모르겠지만 일단 이걸로 써보았다. 참고로 국민총소득이든 생산세가 제외되는 요소비용국민소득이든 결과는 크게 다르지 않더라)
이를 한국은행 경제통계시스템 ECOS에서 10. 국민계정 > 10.1.1. 연간지표 > 경제규모 및 국민소득(명목) > 국민총소득(명목, 원화표시)에서 GNI를 구했으며, 10. 국민계정 > 10.3. 생산, 지출, 자본, 국외거래(종합계정) > 10.3.2. 국민처분가능소득과 처분(명목, 연간) > 10.3.2.1. 국민처분가능소득과 처분(명목, 연간)에서 고정자본소모율을 구했다.
근로시간의 경우 15.6. 고용, 임금, 가계, 사회 > 15.6.6. 산업별 근로일수 및 근로시간, 임금총액(5인 이상)에서 전체근로시간을 구했다. 이걸 구하고보니 백 단위란 걸 알게 되었고 고용노동부 고용통계에서 월평균 근로시간이란 것을 알게 되었다... 그래서 총 근로자 수를 고용노동부 고용동향에서 얻은 후
총 근로시간 = 월평균 근로시간 × 12 개월 × 총 근로자 수
이렇게 해서 얻었다. 기간범위는 2000년부터 2015년까지이다.
검증
변수가 두 개밖에 없으니 간단하게 R을 이용하여 모형평가를 시행할 수 있었다. 결과는.. 의외로 좋게 나와서(?) 의심스러운 상황이다.
먼저 이 결과를 해석하기 이전에 노동시간의 화폐적 표현을 정의하자.
$\mu=\frac{p(I-A)x}{lx}$

다음으로 통계 결과에 대해 해석해보자.
우선 회귀계수 Coefficients는 다음과 같다.
$Lx=1.830_{E+04}+5.821_{E-03}P(I-A)x$
$P(I-A)x$가 0에서 정의되는 절편이 18300이고, $P(I-A)x$에 곱해진 회귀계수 $0.005821$은 직접노동량 $lx$를 예측할 수 있게 해준다고 볼 수 있다. 그렇다면 어느정도로 잘 맞아떨어질까?
그것이 결정계수 R-square로 알 수 있다. R제곱은 0과 1사이이며 1에 가까울 수록 회귀선에 근접한 정도를 나타낸다. 결과는 0.9718. 매우 놀라운 예측력을 갖고 있다는 걸 알 수 있다.
그런데 회귀분석이 예측 값과 실제 값의 차로 나타나는 잔차 $\epsilon$의 정규성이 성립하는 걸 전제로 하는 데... Q-Q Plot 및 히스토그램으로 확인해본 바로는 정규성이 불확실해 보인다. 뭐야 이럴 땐 어떻게 하지?ㅋㅋ
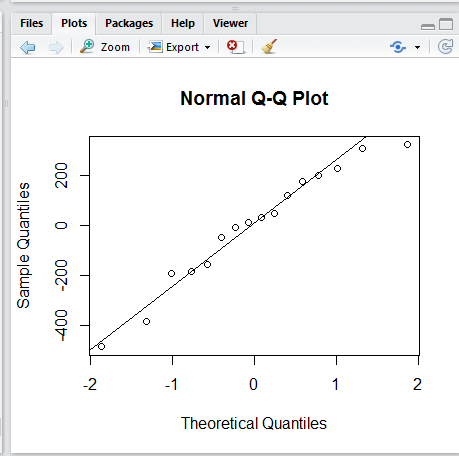
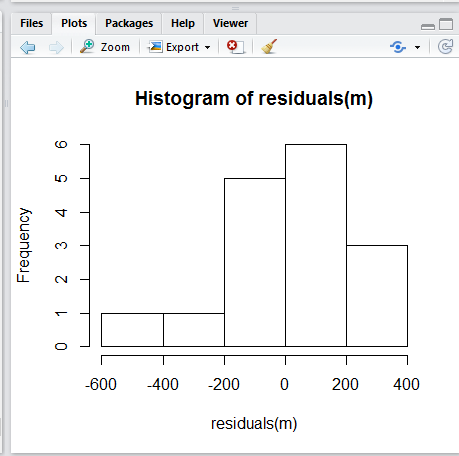
좀 더 공부해보는 것으로... OTL
[이관 글. 2017-01-31 작성]
'정치경제학' 카테고리의 다른 글
| MELT의 잔차 분석 (0) | 2021.05.24 |
|---|---|
| 생산적 노동의 구분 문제에 관한 노트 (0) | 2021.05.24 |
| 절대적 잉여가치와 상대적 잉여가치 (1) | 2021.05.23 |
| 뒤메닐의 이윤율에서 스톡과 플로우 문제에 관하여 (0) | 2021.05.23 |
| 불균형 미시경제학과 합리성, 그리고 차원의 불안정성 (0) | 2021.05.23 |

